Research

Turing's diffusion-driven instability is a widely used canonical model for pattern formation in biology. The basic Turing model consists of two coupled diffusion-reaction partial differential equations. Traditionally, the model is posed on a fixed domain. Depending on the kinetic terms and the parameters, the typical resulting patterns are spots, and/or labyrinthine stripes.
However, many stripe patterns observed in biology are not disordered labyrinths, but instead they are aligned along a specific direction. Consider a zebra: the stripes along most of its body are vertical. What mechanisms can cause this kind of robust directionality and alignment?
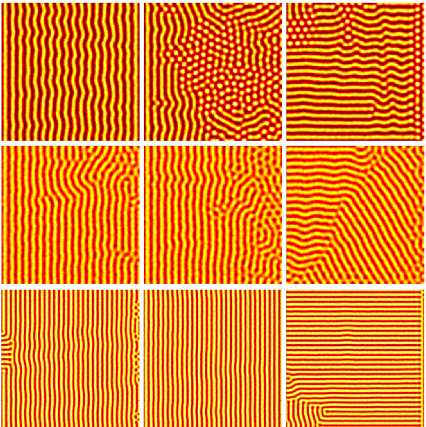
A wave of competency refers to a phenomenon where the region where patterning is possible expands out like a wave, usually due to maturation of the underlying tissue. We show that it is possible to select a preferred alignment and directionality of the stripe patterns by modulating the wave speeds. Moreover, this holds true for multiple different models. In the figure on the left, the columns from left to right corresponds to decreasing wave speeds. We postulate that this mechanism can explain the stripes found in many biological systems, and the wave of competency can be used to control the patterning process, in order to obtain a desired pattern.

Related publications: [1](arXiv)

The Fisher-KPP model is a simple reaction-diffusion partial differential equation that exhibit travelling wave behaviour. It has been used to model a variety of biological phenonmena, such as cell invasion, wound healing, the spread of advantageous mutations, and the behaviour of invasive species. The model has since been generalized to have a more complicated kinetic terms, which has additional parameters to allow better fitting of experimental data.
However, as the model becomes more complicated, the issue of parameter identifiability becomes a concern, since more data is needed to pin down the best values of the parameters. In this project, we explore some of the factors that can impact parameter identifiability in generalized Fisher-KPP models, and the implications of these results toward model selection.

Related publications: (arxiv)

Not all data are equal when it comes to parameter identifiability. A well-designed experiment can provide data that are more helpful for the purpose of pin-pointing parameter values in a model. The goal of this project is to systematically design the optimal experiment that yields the most useful data. We use cell invasion assays as an example. First, we discuss the most suitable initial condition to the experiment, both in the theoretical case with few constraints, or in the practical case where only initial conditions of some special form are easily achievable. Next, we consider modifying the experiment by introducing a control variable, which can be adjusted to maximize the impact of variation in parameter values on model solutions. The results are also applicable to model selection, where we need to differentiate between models that do similarly well as reproducing experimental data.

In many modelling applications, we are not only interested in predicting the behaviour of the underlying system, but also in controlling the system and guiding it toward certain desirable outcome in an efficient way. This can be done by manipulating certain aspects of the system, which are called control variables. For models that takes the form of ordinary or partial differential equations, there exist well-developed techniques, such as Pontryagin's Maximum Principle, and Bellman's Equation, to find the optimal way of manipulating the control variables. However, for agent-based models, there are currently no applicable techniques to do the same. Here, we try to develop a machine-learning based approach, combining ideas from equation learning and dimension reduction, to produce a method for calculating optimal control for agent-based models.

Many types of eukaryotic cells have the ability to crawl. This is crucial for many many biological functions, an example is the migration of neural crest cells. In a vertebrate embryo, a plate of cells (called the neural plate) folds up to form the neural tube, which is the precursor to the brain and spinal cord. Right at the point where the tube closes up is a group of cells called neural crest cells. They will migrate a long distance to various places in the embryo, eventually forming a variety of tissues. Without the ability to crawl, they wouldn't be able to get to where they are needed.
The crawling action is done by extending in the front via actin polymerization, and contracting in the back suing myosin motors. The actin cytoskeleton, and the myosin motors, are controlled by a large group of signalling proteins, some key members among them belongs to the family GTPases.
We are interested in the spatio-temporal distribution of the GTPases. In order for the cell to be able to crawl, the distribution of GTPases must be robustly polarizable, that is, we need it to be high on one end of the cell and low on the other, and stay that way. The wave pinning model was developed to describe the dynamics of GTPases.
In our study, we analyzed the wave pinning model with the Local Perturbation Analysis (LPA) technique, to determine conditions under which polarization is possible. We also couple the model with cells that can grow and shrink in response to GTPase activities, to see if this model can reproduce the crawling action of the cells. The figure on the left shows a cell deformed under the effect of GTPases.

Related publications: [1] [2] [3]

Childhood absence epilepsy (CAE) is a type of epilepsy that causes patients to have sudden and frequent absence seizures ("blank out"). It usually manifests in young children between 4-6 years old, who eventually grow out of it in their later years. We would like to understand the mechanisms behind the seizures, and why CAE only affect young children. This important for predicting when will seizures occur, and also for developing ways that can prevent the seizures from happening.
To do so, we consider a simple system consisting of three types of neurons (RT, TC, and CT as shown on the top diagram on the left), and represent their dynamics with a conductance-based model (Hodgkin-Huxley). It has been known that CAE patients have weaker connections between these neurons compared to healthy people, however that fact alone does not explain CAE, since the connections does not get stronger as the patients get older and grow out of CAE.
We believe a key mechanism is conductance delay. The CT and TC neurons are located far apart in the brain, thus it takes some time for a signal to travel from one neuron to another. This time delay is longer in young children compared to adults, since their nervous systems (especially myelin sheath) are not fully mature. To account for this fact, we add delay terms to our model. We were able to show that, a long conductance delay, in conjunction with weaker connections, results in a bistable system consisting of two stable states. In the lower diagram on the left, we show that in this case, it is possible to switch between these two states as the result of small perturbations.
However, with either a short conductance delay, or stronger inter-neuron connection, one of the two state is destabilized. We therefore believe the remaining stable state represents normal brain functioning, and the destabilized state represent seizure. This can explain why seizures occur in CAE patients, and why they can grow out of it as their myelin sheath matures due to age.

Related publications: [1]