 |
 |
 |
 |
Effects of domain growth on a model pattern generator
An obvious characteristic of embryonic tissue is that it grows, yet, surprisingly, comparatively little analysis has been carried out to investigate the effect of domain growth in mathematical models for pattern generation. We have reformulated on a growing domain the Turing reaction-diffusion model for spatial pattern formation and used a combination of numerical simulation and analysis to determine modes of pattern transition due to domain growth.
In publication 109, we show that growth can greatly enhance the reliability of pattern selection thus overcoming a major criticism of the Turing model. In publication 133 we consider a generic reaction kinetic scheme and using a piecewise linear approximation we find closed form approximate solutions for the steady-state patterns by exploiting a small parameter, the ratio of the diffusion coefficients, in a singular perturbation expansion on an exponentially growing domain. This allows us to determine when transitions (mode doubling) occur in the pattern sequence and what form they will take (insertion of new peaks or splitting of existing peaks). We also show the possibility of a novel sequence behaviour, mode-tripling.
In publication 141 we generalise our results to the case of spatially non-uniform growth and in 139 we use the model to examine growth patterns of the ligaments of arcoid bivalves (marine molluscs). We show that strikingly different patterns can arise from the same development program allowing us to draw conclusions on the evolutionary relationship between different families of molluscs.
In publications 57 and 67, we use an extended version of the above model to account for the complex spatiotemporal sequence of tooth primordia generation in the alligator jaw.
 |
 |
 |
 |
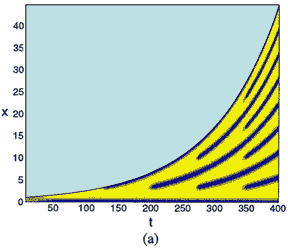
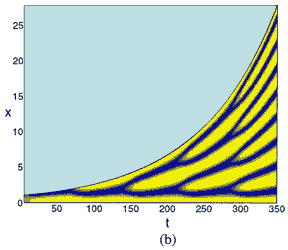
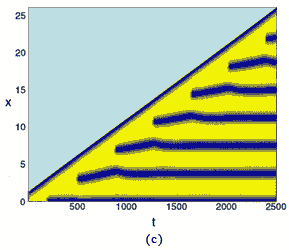
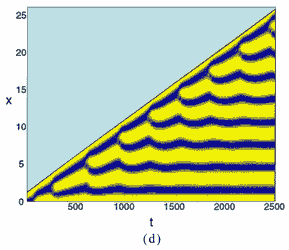
Patterns in activator concentration on a one-dimensional uniformly exponentially growing domain exhibiting mode doubling via (a) peak insertion, and (b) peak splitting. On a non-uniformly growing domain (for example apical growth) new patterns are generated at the growing tip by a similar mechanism, namely (c) peak insertion, and (d) peak splitting. [Reproduced with permission from publication 141].
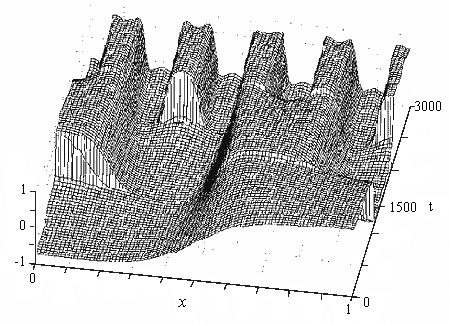 |
A novel form of pattern sequence generation involving mode-tripling on an exponentially growing domain rescaled to [0.1].[Reproduced with permission from publication 133].
** Work carried out in collaboration with E.J. Crampin, E.A. Gaffney and W.W. Hackborn