Lattice and discrete Boltzmann
equations for fully compressible flow
P. J. Dellar (2005) Lattice and
discrete Boltzmann equations for fully compressible flow, pages
632-635 of Computational
Fluid and Solid Mechanics 2005,
Proceedings of The Third MIT Conference on
Computational Fluid and Solid Mechanics, edited by K.-J. Bathe and
published by Elsevier.
Reprint as Adobe PDF (109K)
Abstract
Equilibria for the common two-dimensional,
nine-velocity (D2Q9) lattice Boltzmann equation are not uniquely
determined by the Navier--Stokes equations. An otherwise undetermined
function must be chosen to suppress grid-scale instabilities. By
contrast, the Navier--Stokes--Fourier equations with heat conduction
determine unique equilibria for a one-dimensional, five-velocity (D1Q5)
model on an integer lattice. Although these equilibria are subject to
grid-scale instabilities under the usual lattice Boltzmann streaming
and collision steps, the equivalent discrete Boltzmann equation is
stable when discretized using conventional finite volume schemes. For
flows with substantial shock waves, stability is confined to a window
for the parameter controlling the mean free path. It is constrained
between needing a large enough mean free path (large enough viscosity)
to provide dissipation at shocks, and a small enough mean free path to
ensure valid hydrodynamic behavior.
Typos
Three fairly obvious typos unfortunately survived the proof-correcting
process in the published volume, but are corrected in my PDF version
linked to above.
The first of equations
(2) should be 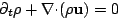 , while equation (6) was missing a minus
sign in the exponent,
, while equation (6) was missing a minus
sign in the exponent, 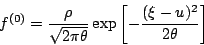 .
.
Equation (8) should read 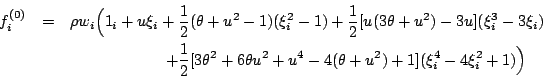
so that the quartic moment agrees with equation (7).
@InProceedings{Dellar3rdMIT,
author =
{P. J. Dellar},
title =
{{Lattice and discrete Boltzmann
equations for fully compressible flow}},
booktitle
= {Computational Fluid and Solid Mechanics 2005},
pages =
{632--635},
year =
{2005},
editor =
{K.-J. Bathe},
organization = {Proceedings of
The Third MIT Conference on Computational Fluid and Solid Mechanics},
publisher
= {Elsevier},
address =
{Amsterdam}
}
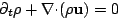 , while equation (6) was missing a minus
sign in the exponent,
, while equation (6) was missing a minus
sign in the exponent, 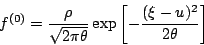 .
.