 |
 |
 |
 |
 |
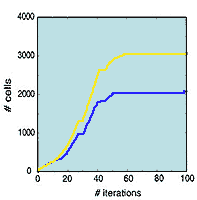 |
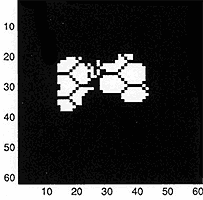
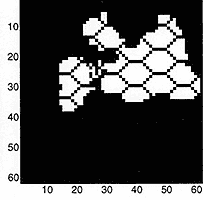
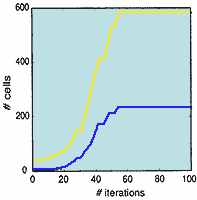
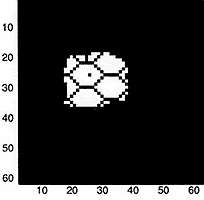
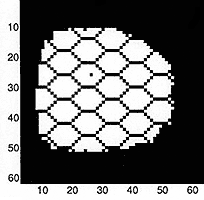
Simulations showing the evolution of the spatial distribution of cells for growth in inhomogeneous (top panels) and homogeneous (bottom panels) environments. The white spaces are occupied by cancer cells, the black spaces are either empty or occupied by the (hexagonal) array of blood vessels (a highly idealised vascular network). The graphs show the time evolution of the number of cancer cells for each case. The yellow lines denote total number of cancer cells (proliferating + quiescient) while the blue lines denotes number of quiescient cells. Note the order of magnitude difference in scale. In each case the normal cells tend to zero.
 |
 |
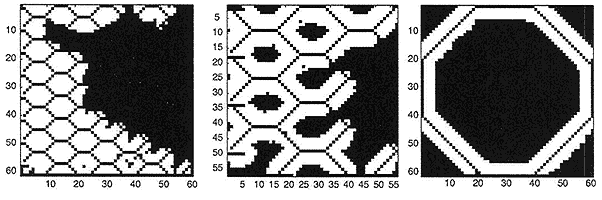 |
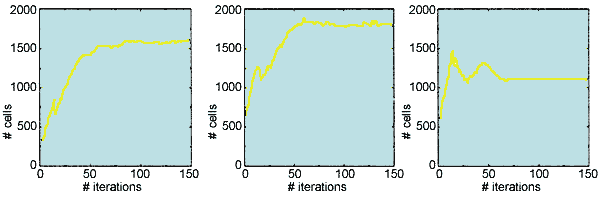
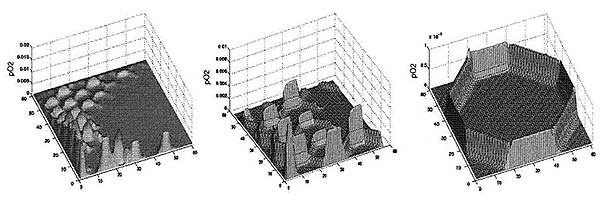
Simulations for vascular networks of different sparsity. First row corresponds to time evolution of the cancer colony, where each iteration represents 15 hours; second row shows the stationary distribution of oxygen concentration, and the third row shows the stationary distribution of cells (see above). [Reproduced with permission from publication 165]
** Work carried out in collaboration with T. Alarcon and H.M. Byrne