$\newcommand{\Hepp}[1]{\mathcal{I}^{\text{tr}}_{#1}}\newcommand{\Period}[1]{\mathcal{I}_{#1}}\newcommand{\ind}{a}\newcommand{\td}{\mathrm{d}}\newcommand{\Z}{\mathbb{Z}}\newcommand{\set}[1]{\{#1\}}\newcommand{\GRT}{\mathsf{GRT}}\newcommand{\Gmot}{\mathsf{G}^{\text{mot}}}$ grant URF\R1\201473 (Royal Society)

Quantum perturbation theory at large orders

The recent Higgs discovery is merely one further mark of the spectacular success of the standard model of particle physics. Yet the underlying mathematical foundations of quantum field theory (QFT) are only poorly understood. Even after decades of dedicated research, a rigorous construction of the quantum Yang–Mills theories underlying the standard model is still an open Millenium Problem. The quest to solve these mysteries inspired research and progress in many branches of mathematics, including commutative and noncommutative geometry, topology, combinatorics, representation theory, probability, functional analysis and number theory.

Perturbation theory describes quantizations as small deformations of classical or free systems that are well understood. It produces power series that for example predict the particle interactions at high energies. The traditional techniques for such calculations are exhausted, and even with modern computers, progress is only possible through the development of new mathematics. This very active area of research at the cutting edge of theoretical physics and mathematics is transferring ideas between these disciplines and has already led to exciting new insights in both.

The long-term goal of my research is to solve the fundamental problems of QFT by advancing perturbation theory. My work [PW] with Wulkenhaar shows how high order perturbation series led to the first solution of an interacting theory in 4 dimensions [GHW]; I strive to achieve the same in physical theories. Over the next years, my contributions to this program will include: This research sits at the interface between pure mathematics, theoretical physics and computer science. I will develop new mathematical techniques drawing on tropical geometry, $D$-modules and motivic Galois theory. The outcomes consist of theorems, but also data and effective methods and algorithms that will be useful and readily available for the wider scientific community.

1. Tropical quantum field theory

Elementary particle interactions are encoded as combinatorial graphs $G$ called Feynman diagrams. Each diagram defines a Feynman integral $\Period{G}$, which is a function of particle masses, momenta, and regulators including the dimension of space-time. A fundamental challenge is the ever growing complexity of these functions, which limits calculations to low orders in perturbation theory.

I developed a variant [P1] of Feynman integrals that assigns a rational function $\Hepp{G}$ to a Feynman diagram. It is defined by replacing the operations `+' and `·' of addition and multiplication by `max' and `+'. This is a drastic simplification, but the idea behind tropical geometry is that at least some interesting information is retained. In fact, it works extremely well; the integral $\Period{G}$ is predicted within 1% precision from $\Hepp{G}$ through a smooth interpolating curve. For the Feynman diagrams at 7 loops in $\phi^4$ theory, this is shown in the following figure:

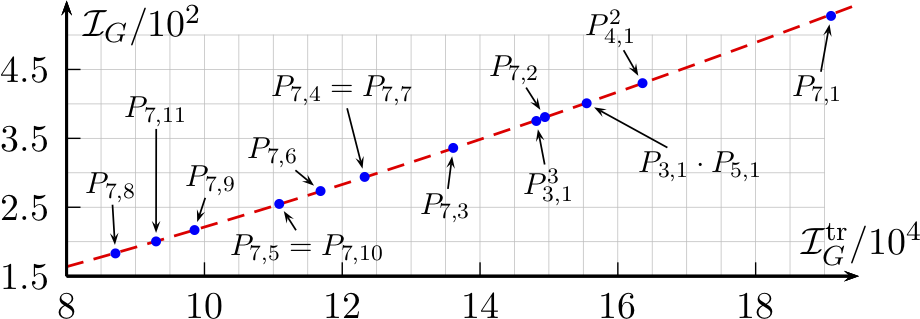
7 loop plot (tropical vs. Feynman integrals)

This strong correlation shows that the tremendous transcendental complexity of Feynman integrals can be captured to high accuracy by their tropical analogues. This opens unprecedented opportunities to explore Feynman integrals at large orders and to study resummation. By incorporating kinematics and dimensional regularization, the set of tropical Feynman integrals constitutes a perturbative QFT. It has the same structure of divergences as the original physical theory, it is renormalized in exactly the same way, and even numerically it gives very similar values. I will explore to which extent this tropical theory can be regarded as a meaningful quantum theory in itself, but already as a model it is very fruitful and enables numerous projects:

The tropical perturbation series have rational coefficients and can be computed to arbitrary order. This will give valuable insights into the resummation problem. Resummation is the process of combining the (first few) coefficients of a divergent, asymptotic perturbative series into (an approximation of) the quantity of interest. The theory of resurgence has developed sophisticated techniques to tackle this problem, but in QFT their implementation is frustrated by the very small number of available coefficients. In practice, resummation relies on heuristics and unproven, barely tested assumptions.
In [KP] we showed that the large, uncontrolled uncertainties within these resummation procedures severely limit the utility of higher order perturbative corrections. With the tropical model, I can for the first time test the underlying assumptions, identify suitable resummation procedures and determine the errors. These improvements are crucial to obtain accurate predictions from perturbation theory, and to make contact, for example, with recent bootstrap calculations. The number $\Hepp{G}$ is the volume of the polar of the spanning tree polytope and can be approximated for hundreds of orders in perturbation theory by rapidly mixing random walks [EF]. I will explore the log-concavity of graph polynomials and apply these walks directly to Feynman integrals $\Period{G}$ to obtain high precision estimates, even better than from the plot above, and at higher orders. For recent developments along these lines, due to Michael Borinsky, see [B].

Remarkably, the tropical integral also detects all known identities of Feynman integrals. In fact, it suggests new identities not explained by any known relations [P1].

Conjecture: For two graphs, we have $\Period{G_1}=\Period{G_2}$ if and only if $\Hepp{G_1}=\Hepp{G_2}$.

Symmetries are fundamental in physics, and understanding these new relations will reveal a hitherto missed symmetry.

2. Difference equations and generating series of periods

The number of Feynman diagrams grows factorially with the order in perturbation theory. It is essential to reduce the number of integrals by several orders of magnitude. This reduction to master integrals is a crucial limiting factor. The Feynman integral is the Mellin transform \begin{equation*} \Period{G}(\vec{\ind}) = \left( \prod_{i=1}^n \int_0^{\infty} x_i^{\ind_i-1} \td x_i \right) P^{-d/2}(x) \qquad\text{of the sum}\qquad P=\mathcal{U}+\mathcal{F} \end{equation*} of the Symanzik polynomials. Shifts $\Period{G}(\vec{\ind} + \vec{c})$ of the regulators $\vec{\ind}$ by integers $\vec{c}\in \Z^n$ are subject to contiguous relations, like hypergeometric functions. All these shifts span a finite dimensional vector space. By work of Loeser—Sabbah, its dimension (number of master integrals) equals the Euler characteristic of the surface $\set{P=0}$ and is computable in all cases of interest [BBKP].

To solve the reduction problem, I will determine the matrices representing the basic shifts $\vec{\ind} \mapsto \vec{\ind} + \vec{e}_i$ along coordinate directions. With these at hand, the reduction of an arbitrary shift $\Period{G}(\vec{\ind}+\vec{c})$ trivializes to a sequence of matrix multiplications. This proposal is radically different from established methods, which suffer from a severe increase in complexity with each additional shift. I already succeeded with the new approach in first examples, and I will develop the theory further and exploit the recursive structure of the face lattice of the Newton polytope of $P$. Such complete control of difference equations is very useful in mathematics, for example to prove arithmetic recurrences like Beukers' and Apéry's sequences from irrationality proofs.

A further implication of regulators is that the Mellin transform $\Period{G}(\vec{\ind})$ becomes a generating series for infinitely many periods, upon expanding $x_i^{\ind_i} = \sum_{k} (\ind_i \log x_i)^k/k!$. Each such coefficient is typically considered individually and gives ever more involved integrals with growing $k$. This inefficient approach obfuscates an important structure: The motivic Galois theory of the generating series as a whole admits a concise description, encoding information about its infinitely many coefficients [ABDG], [BD]. The techniques [P2] of fibrations by marked genus 0 curves extend to twisted cycles and can be applied directly to the entire generating series. In the cases where suitable fibrations exist, this exciting theory will allow proofs and direct calculations of motivic coaction formulas of generating series. It also solves the difference equations from above and gives an algorithm to construct bases of uniform transcendentality, which simplify the period calculations for high logarithmic powers $k$ drastically.

3. Deformation quantization

In his seminal 1997 paper, Kontsevich solved a major problem in canonical quantization and gave a universal perturbative quantization formula for arbitrary Poisson structures. It remained practically intractable for 20 years, due to the complexity of the corresponding Feynman integrals. We recently gave an effective algorithm for their calculation, proving that they evaluate to multiple zeta values [BPP]. The next goal is to show the convergence of this perturbation series. This is joint work with Brent Pym. We have identified the integrals that conjecturally dominate the asymptotic behaviour of the series, but to obtain a proof, further research is needed to adapt the asymptotic methods inspired by the tropical Feynman integral to Kontsevich's setting.

Another direction of our project is the mysterious connection between the Grothendieck—Teichmüller group $\GRT$ and Brown's motivic Galois group $\Gmot$ of multiple zeta values: $\GRT$ acts on associators and quantizations by work of Dolgushev and Willwacher [W]; $\Gmot$ acts on the coefficients by our theorem. This suggests a new action of $\Gmot$ on quantizations.

References