Phase Transitions of the Regular Polytopes and Cone
Some sparse approximation questions can be modelled exactly through convex polytopes. When this is possible, their analysis can provide Precise Undersampling Theorems (by Donoho and Tanner). These results are cast in terms of the:
Over-sampling ratio: δ = n/N,
Under-sampling ratio: ρ = k/n,
where k is the sparsity of the vector, n is the number of measurements and N is the length of the vector measured.
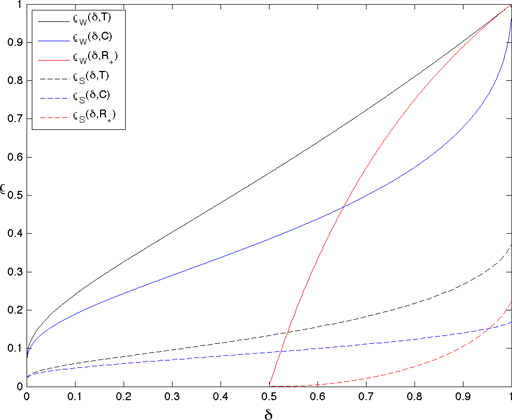
This form interpolates the values of the strong and weak phase transitions of the orthant and three regular polytopes: the simplex, crosspolytope, and hypercube as well as the orthant. For ρ below a strong phase transition, the phenomenon is true for all k-sparse vectors, and below a weak phase transition, the phenomenon is true for most k-sparse vectors. The crosspolytope models l1-regularization, the simplex models l1-regularization with nonnegativity (or other sparsity constraints) and uniqueness of nonnegative vectors when the average of the signal is also measured, the orthant models uniqueness of nonnegative vectors from mean-zero measurement matrices, and the hypercube models bound constrainsts where k is the number of entries in the vector which are not at the bounds. The figure below shows these plots for the crosspolytope (blue, C), simplex (black, T), orthant (red, R+) and hypercube (only weak phase transition, solid red, R+). For further details see Precise Undersampling Theorems (by Donoho and Tanner). Tabulated values of these phase transition are available in MATLAB format.