|
|
|
Cellular Swimming --Bacterial Motility. Boundary Accumulation. H Shum, EA Gaffney, DJ Smith, Modelling bacterial behaviour close to a no-slip plane boundary: the influence of bacterial geometry, Proc Roy Soc A (2010) 466 p1725-1748.
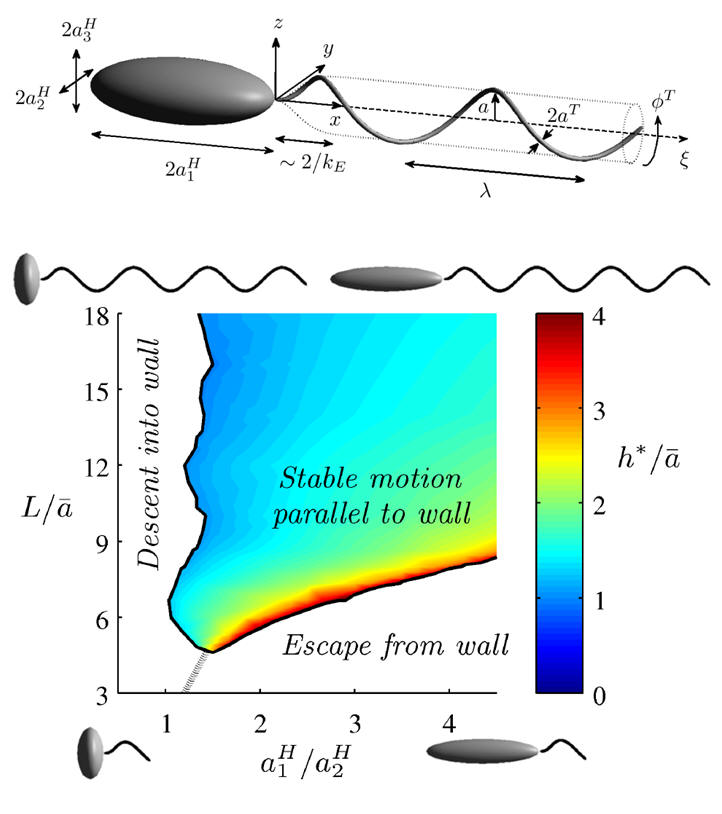
Bacteria are observed to accumulate near boundaries, a necessary step in the initiation of a biofilm, which are responsible for biofouling and biodeterioration of water distribution and treatment systems, heat exchangers, filters, and medical implants as a few selected examples. Bacterial motility is generally observed to be important in the initiation of biofilms though the mechanics of how bacteria reach surfaces is underexplored. Lauga et al (2006) unravelled the mechanics behind observations that bacteria swim in circles close to a surface and demonstrated that bacteria will descend into a wall. However, stable surface swimming is also observed. In this study we consider the surface swimming dynamics of a canonical monotrichous (singly flagellated) bacterium, based on Rhodobacter Sphaeroides. In particular we have demonstrated that spherically headed bacteria will descend into a wall, matching Lauga et. al.'s predictions. Further, as the geometry of the bacterial cell body and its flagellum are varied stable surface swimming, wall descent and surface escape can all occur. Given the wide biodiversity in bacterial geometries, this emphasises that motility alone does not give the complete picture for the physics of biofilm initiation even before biological factors are considered.
--Sperm Motility. Detailed Image Capture. DJ Smith, EA Gaffney, H Gadelha, N Kapur, JC Kirkman-Brown, Bend propagation in the flagella of migrating human sperm, and its modulation by viscosity, Cell Motility & The Cytoskeleton (2009), 66, 220-236.
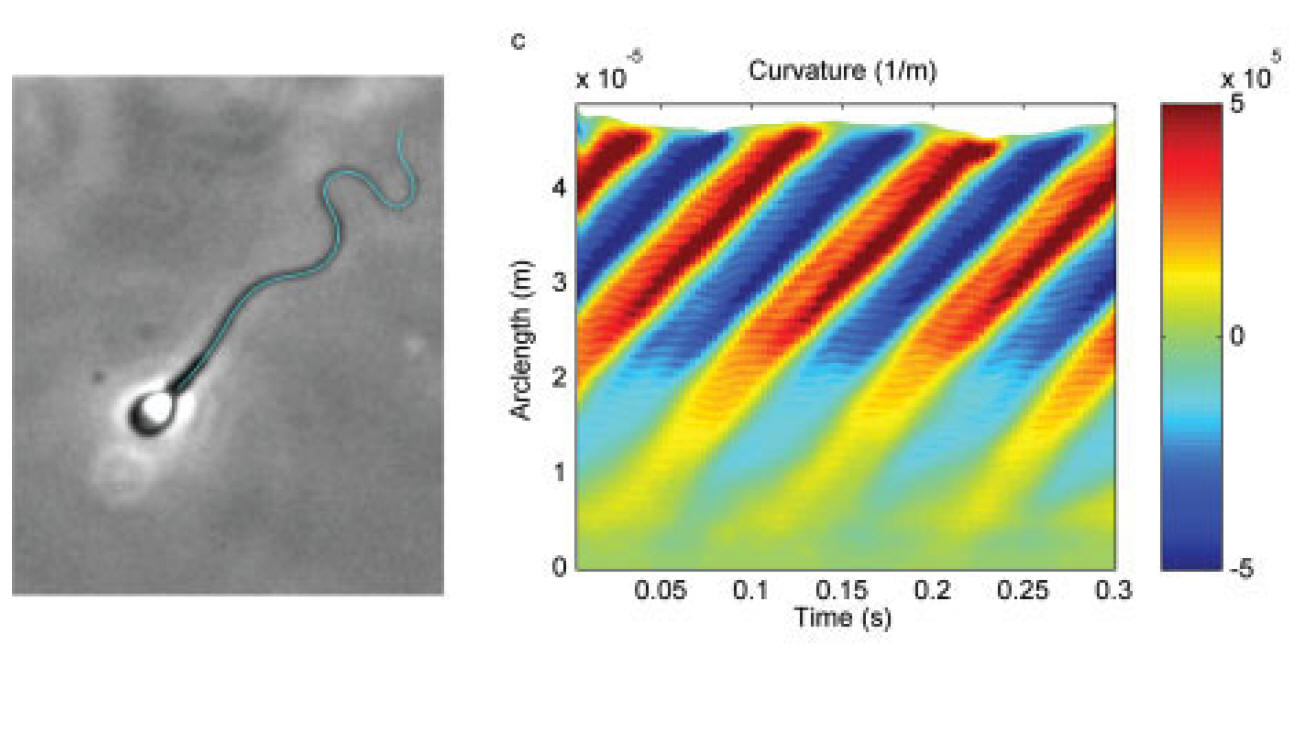
By capturing high resolution movies of swimming human sperm, the changes in the behaviour of their beat patterns can be documented and explored. In particular, even small amounts of media elastc recoil lead to a breakdown of the scalings associated with Newtonian fluid dynamics, emphasising the importance of exploring cellular swimming in viscoelastic media.
--Sperm Motility. Flagellar Instabilities. H Gadelha, EA Gaffney, DJ Smith, JC Kirkman-Brown, Nonlinear instability in flagellar dynamics: a novel modulation mechanism in sperm migration?, J. Royal Society Interface (2010), doi:10.1908/rsif.2010.0136
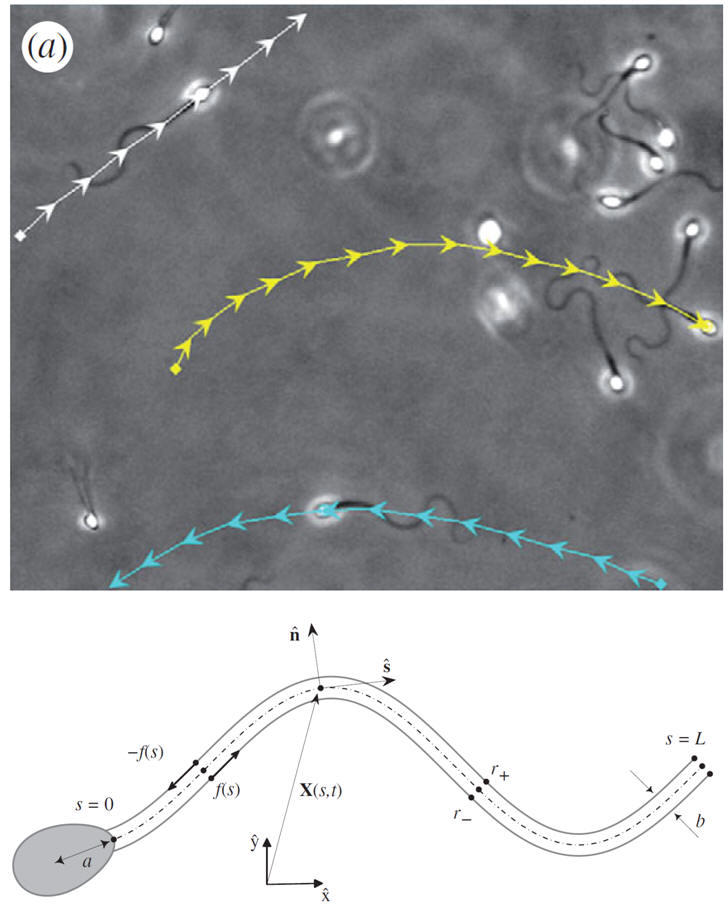
Sperm motility is an emergent property arising from the interaction of its flexible flagellum (tail) with the hydrodynamic drag of the surrounding medium, ultimately being forced by molecular motors generating shear within the flagellum. Sperm are often observed to swim in circles adjacent to boundaries and this can be due to many factors, including cell rolling, an asymmetric cell head, a particular form of beat pattern known as hyperactiviation, or, possibly, hydrodynamic interactions with the surface. On the left are non-rolling human sperm in a highly viscous medium (with a small element of viscoelasticity). There is no hyperactivation, cell rolling nor any cell head asymmetry (due to the use of human sperm as opposed to say mouse). The cells are circling clockwise, anticlockwise and swimming in straight paths, ruling out hydrodynamic interactions with the surface. The question therefore is: why are some cells swimming in circles; what is breaking the symmetry which can be observed to due to asymmetric patterns in the emergent flagellar waveform. We demonstrate that no intrinsic asymmetry is required, whether due to signalling (particualrly calcium which is critical in sperm dynamics) or subtle asymmetries in the structure of mammalian flagella. In particular, asymmetric trajectories can emerge simply from dynamical buckling instabilities for a sufficiently viscous surrounding medium, illustrating that one must be careful in assigning a biological relevance to observations of curved trajectories in chemotactic assays for example.
--Sperm Motility. Slender Body Theory and Boundary Accumulation. DJ Smith, EA Gaffney, JR Blake, JC Kirkman-Brown, Human sperm accumulation near surfaces: a simulation study, J. Fluid Mechanics (2009), 621, p289-320.
Sperm have been observed to boundary accumulate since the studies of Lord Rothschild FRS in the 1960s though the associated mechanics has been relatively underexplored.
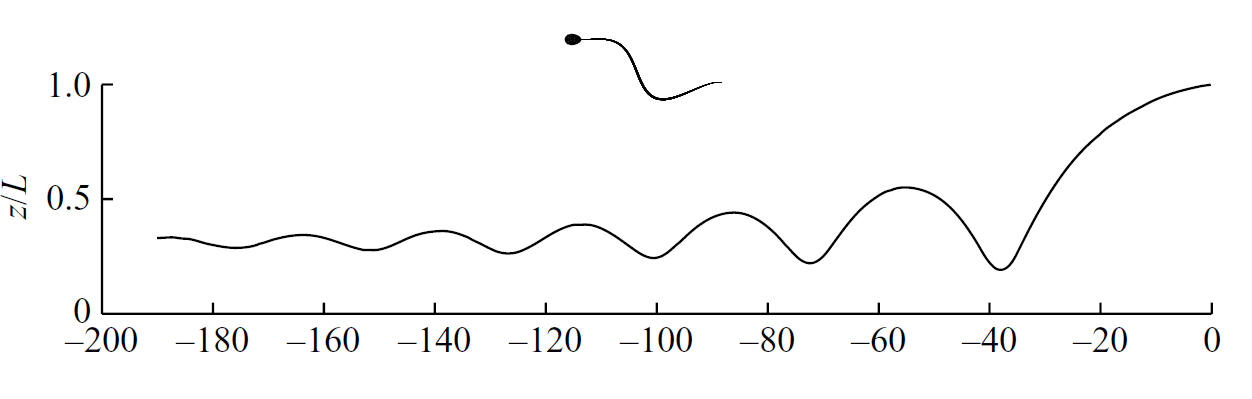
In a simulation study, we have for example demonstrated that simple planar flagellar motions are sufficient to induce boundary accumulation. The simple sinusoid waveform indicated in the sperm caricature induces boundary accumulation as depicted by the damped wave with the sperm moving from right to left with increasing time.
Viscoelastic Singularities and Slender Body Theory.
DJ Smith, EA Gaffney, JR Blake, Mathematical modelling of cilia-driven transport of biological fluids, Proceedings of the Royal Society A (2009), 465, p2417-2439.
Sngularities are derived for a linearly viscoelastic fluid allowing the formulation of a slender body theory for a Maxwell fluid; the above expression is the generalisation of the Stokeslet. The influence of elastic recoil in ciliary induced transport is explored in the simple setting of an individual cilium, with the beat pattern as depicted. In particular transport levels are very sensitive to elastic recoil suggesting that the release of large chain molecules into periciliary fluid of the lung airway surface liquid, as occurs with asthma, have the potential to induce an adverse effect on mucociliary transport.
Modelling Fibroblast Growth Factor Signalling
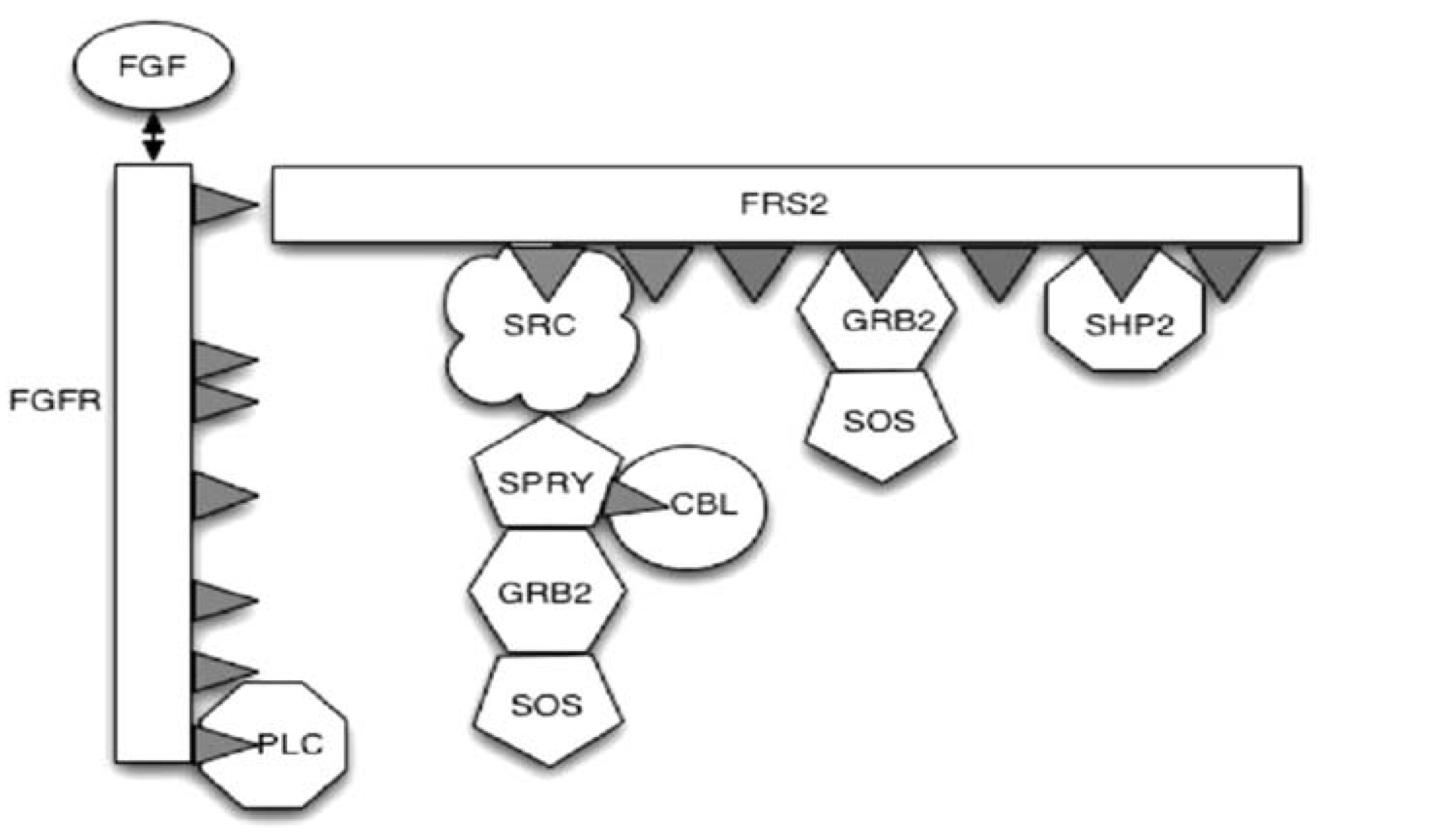
EA Gaffney, JK Heath, MZ Kwiatkowska, A Mass Action Model of a Fibroblast Growth Factor Signaling Pathway and Its Simplification, Bulletin of Mathematical Biology (2008) 68, p99-130.
FGF binds to its receptor which, in complete generality, is one of four receptor tyrosine kinases, FGFR1-FGFR4, with both ligand and receptor classified into different isoforms with varying specificities for each other. Here, the focus is on the initiation of the RAS-MAP kinase pathway which proceeds via the binding of the docking protein FRS2 to activated FGFR. The FRS2 subsequently phosphorylates with the recruitment of multiple binding molecules, including GRB2, the binding of which initiates the desired pathway via subsequent SOS binding. However, other molecules binding FRS2 act to downregulate the FGF signal by a multitude of mechanisms, such as ubiquitination, entailing that the transduced FGF signal is transient. A model of FGF signaling is constructed using the law of mass action and Michaelis-Menton kinetics; hundreds of ordinary differential equations are generated due to an explosion in the combinations of ways molecules may bind to the docking protein FRS2. We demonstrate how this model can be systematically and accurately simplified, reducing run-times by over two orders of magnitude and consider the sensitive dynamics of the binding molecule SHP2. The methods presented here can also be applied to simplifying other signal transduction pathways involving docking proteins.
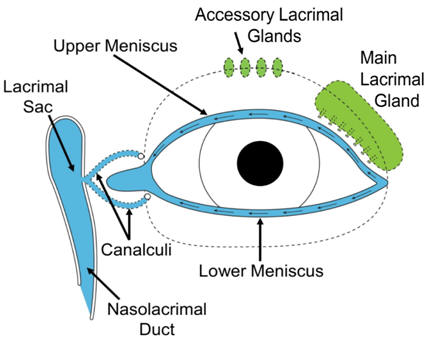
Tear Film Dynamics and Applications to Dry Eye Diagnostics EA Gaffney, JM Tiffany, N Yokoi, AJ Bron, A Mass and Solute Balance Model for Tear Volume and Osmolarity in The Normal And The Dry Eye, Progress in Retinal And Eye Research (2010), 29, p59-78.
The pre-ocular tear film is a stratified incompressible shear thinning
fluid which is a few microns thick and consists of a mucus layer,
covered by an aqueous layer, which is turn covered by an extremely thin
lipid surface layer. It possess a free surface with menisci adjacent to
the eyelids; is secreted by the lacrimal gland. In addition, ocualr surface fluid is lost via evaporation
and drainage at the lacrimal duct and will eventually break-up in the
absence of blinking. Pathologies of this film, or its production, are
typically responsible for dry eye which possesses many features that are
encompassed by fluid mechanical and associated solute transport
processes. In particular hyperosmolarity is considered
to be responsible for dry eye induced ocular surface damage.
However, the solute and fluid dynamics of the ocular surface are still
far from a complete understanding in part due to sampling difficulties
given such a thin film coating of an inherently delicate biological tissue,
restricting detailed measurements to the menisci.
In this paper, a modelling framework is explored which
illustrates, for example, that meniscus based measurements of solute
concentration are only slightly lower than tear film osmolarity for the
normal eye, but can be extensively lower for dry eye. Further, a
combination of two observables, a high meniscus osmolarity and a low
meniscus radius of curvature, is predicted to be highly correlated with
high solute concentrations in the central tear film and thus the
propensity for ocular surface damage. Reaction Diffusion Patterning in Biological Systems Morphological pattern formation is a complex spatio-temporal process producing enormous diversity and yet with relatively few fundamental principles, typically utilising homologous and evolutionary conserved pathways. The primary mechanism driving morphogenesis is differential gene expression, which allows cells with identical DNA to differentially express proteins and thus to create, and respond to, heterogeneous environments in a context dependent manner. The possibility that long range, diffusible, signals, known, as morphogens may initiate biological self organisation via a dynamical instability in response to fluctuations has been explored since Turing's eponymous paper in the 1950s. In particular, extensive theoretical studies have demonstrated that a slowly diffusing autocatalytic morphogen, the activator, interacting with a rapidly spreading antagonistic morphogen, the inhibitor, can induce the emergence of patterning as well as amplifying existing self-organisation (Gierer and Meinhardt, 1972; Segel and Jackson, 1972)
-- The Influence of Domain Growth A Madzvamuse, EA Gaffney, PK Maini, Stability analysis of reaction-diffusion systems with time-dependent coefficients on growing domains, Journal Of Mathematical Biology (2010), 61, p133-164 E. Crampin, EA Gaffney, PK Maini, Reaction and Diffusion on Growing Domains: Scenarios for Robust Pattern Formation, Bulletin Mathematical Biology (1999) 61, p1093-1120.
The basic Turing mechanism is notorious for its sensitivity; for example its predictions of emergent structures are critically dependent on the fine details of fluctuations in initial conditions. This has previously led to suggestions that Turing patterns would not be realised in development (Bard and Lauder, 1974; Bunow et al.,1980). However, when coupled with growth, robust pattern formation can occur without a sensitivity to the initial conditions, via a cascade of instabilities with bifurcations driven by the evolution of the domain. Furthermore, the standard paradigm, of an activator and an inhibitor, is no longer required for growth driven instabilities.
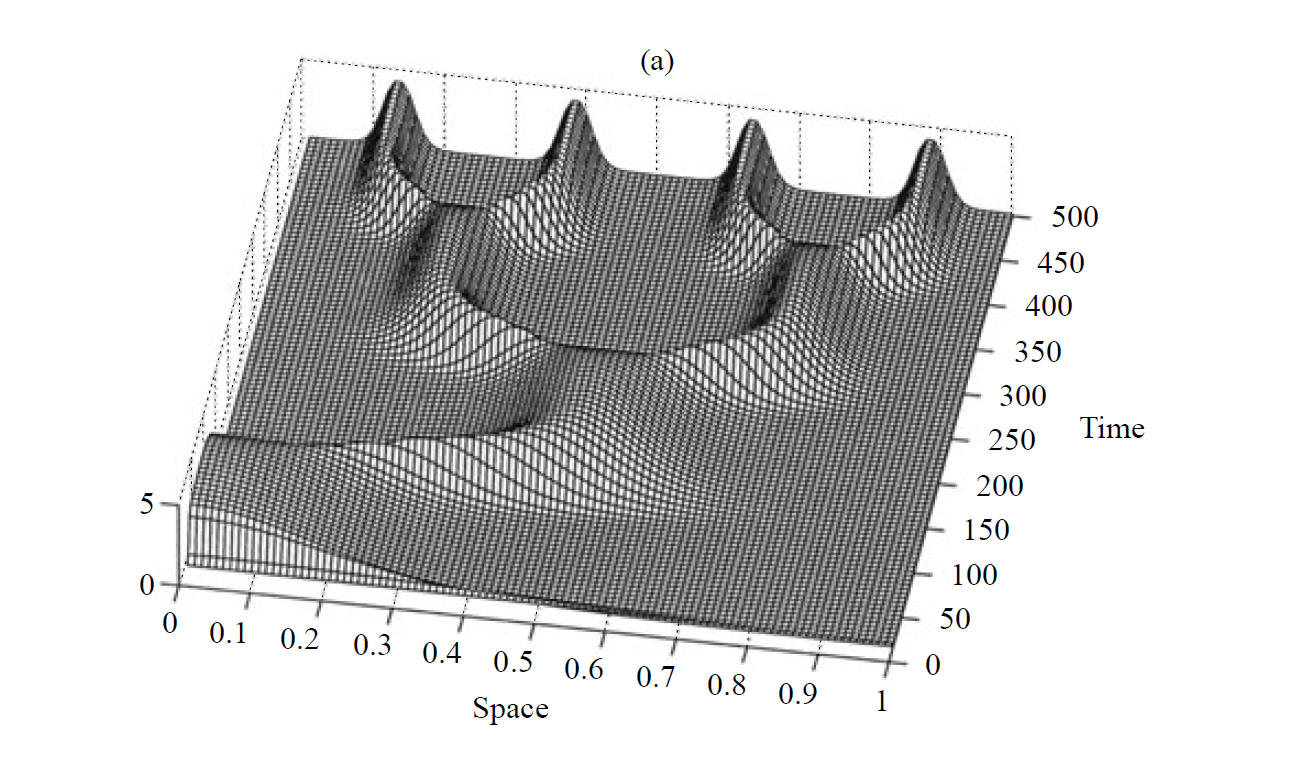
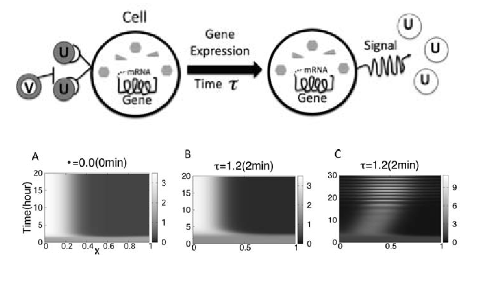
-- The Influence of Gene Expression Time Delays S Seirin Lee, EA Gaffney, Aberrant Behaviours of Reaction Diffusion Self-organisation Models on Growing Domains in the Presence of Gene Expression Time Delays Bulletin of Mathematical Biology (2010), DOI:10.1007/s11538-010-9533-4 S Seirin Lee, EA Gaffney, NAM Monk, The Influence of Gene Expression Time Delays on Gierer-Meinhardt Pattern Formation Systems, Bulletin of Mathematical Biology (2010), doi:10.1007/s11538-010-9532-5
Recent empirical studies reveal that gene expression appears to be fundamental and active in morphogen dynamics for putative Turing systems. However, this introduces temporal delays within the morphogen interaction dynamics implicit in Turing's mechanism. In turn, this generates modelling predictions of aberrant behaviours, such as oscillations in morphogen levels or exquisite temporal sensitivities. Hence the biological relevance of Turing's instability for self-organisation requires a secondary stabilising mechanism if gene expression is also present. More generally, the sensitivity of Turing patterning again appears to cause a discrepancy between observation and prediction, this time with regard to delays implicit in any morphogen interactions.
Modelling Chemotherapeutic Scheduling
-- Palliative Scheduling HC Monro, EA Gaffney, Modelling chemotherapy resistance in palliation and failed cure, J. Theoretical Biology (2009), 257, p292-302.
Chemotherapeutic scheduling models are often based on the premise of maximally tolerated dose. One such protocol which has been motivated by mathematical modelling is Norton's dose densing schedule, which has seen success in recent trials (Citron et al 2002, 2003), though dose densing is not universally successful (Piccart et al 2000). This had led to tentative suggestions that dose densing may be appropriate in the palliative setting (Vasey 2005). However, the dynamics of palliation are fundamentally different especially once irreducible tumour cell resistance is considered. Using the concepts from Luria and Delbruck's famous experiments, which were generalised to the context of cancerous cells by Law (1952), scheduling models predict that dose densing is typically, but not always, inappropriate.
-- The Goldie Coldman Alternation Hypothesis
EA Gaffney, The Mathematical Modelling of Adjuvant Chemotherapy Scheduling: Incorporating the Effects of Protocol Rest Phases and Pharmacokinetics. Bulletin of Mathematical Biology (2005) 67, p563-611. EA Gaffney, The Application Of Mathematical Modelling To Aspects Of Adjuvant Chemotherapy Scheduling, Journal of Mathematical Biology (2004) 48, p375-422.
|
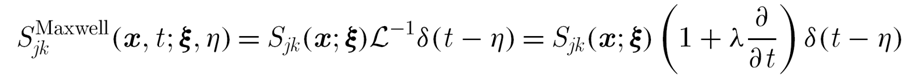
 Numerous
signaling molecules, in the form of secreted hormones or growth factors,
exert their influence via receptor tyrosine kinases, including
fibroblast growth factor (FGF). The motivation for the detailed
investigation of these signaling proteins is not only heightened by
their association with malignant disease, but also because cell
signaling pathways can now be targeted in novel drug discovery programs
(Sevecka and MacBeath, 2006). However,
the mechanisms by which signaling molecules exert their influence on a
cell, and how these can be manipulated and controlled, are not intuitive
due to multiple feedback processes. Consequently, mathematical and
computational modeling have a role in unraveling and simplifying the
complexity of these signaling pathways.
Numerous
signaling molecules, in the form of secreted hormones or growth factors,
exert their influence via receptor tyrosine kinases, including
fibroblast growth factor (FGF). The motivation for the detailed
investigation of these signaling proteins is not only heightened by
their association with malignant disease, but also because cell
signaling pathways can now be targeted in novel drug discovery programs
(Sevecka and MacBeath, 2006). However,
the mechanisms by which signaling molecules exert their influence on a
cell, and how these can be manipulated and controlled, are not intuitive
due to multiple feedback processes. Consequently, mathematical and
computational modeling have a role in unraveling and simplifying the
complexity of these signaling pathways.
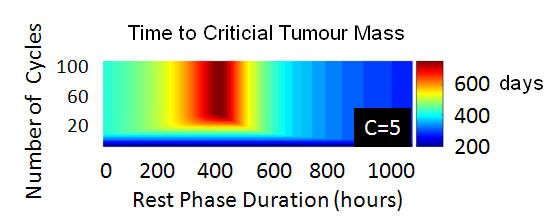
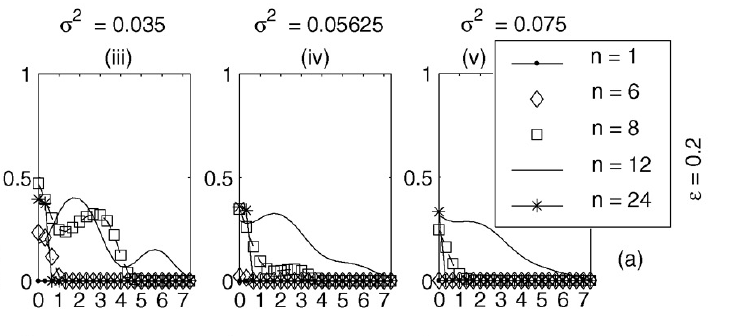 Goldie
and Coldman (1982,1982,1986,1998) considered Luria and Delbruck's
famous experiments for the evolution of resistance in the context
of modelling chemotherapeutic scheduling, developing the well known
hypothesis that treatments not exhibiting cross resistance should be
alternated. However, clinical trials do not generally support these
ideas. The above modelling illustrates that pragmatic complications,
such as the role of the cell cycle and especially pharmacodynamics,
entail that Goldie and Coldman's predictions break down. More
generally, this illustrates that classical modelling studies
on chemotherapeutic scheduling should be tested for robustness with
respect to the inclusion of additional tumour biology and the
complications of drug delivery.
Goldie
and Coldman (1982,1982,1986,1998) considered Luria and Delbruck's
famous experiments for the evolution of resistance in the context
of modelling chemotherapeutic scheduling, developing the well known
hypothesis that treatments not exhibiting cross resistance should be
alternated. However, clinical trials do not generally support these
ideas. The above modelling illustrates that pragmatic complications,
such as the role of the cell cycle and especially pharmacodynamics,
entail that Goldie and Coldman's predictions break down. More
generally, this illustrates that classical modelling studies
on chemotherapeutic scheduling should be tested for robustness with
respect to the inclusion of additional tumour biology and the
complications of drug delivery.