I am a numerical analyst (computational mathematician) primarily interested in numerical linear algebra and related fields. Below is a summary of my current research interests. I am keen to work with motivated students and researchers interested in any of these.

If you are interested in working with me as a Dphil (PhD) student in mathematics, please apply via the Oxford Mathematics website. Feel free to also drop me a line.

Randomized algorithms in numerical linear algebra (RNLA)

This is currently the main focus of my research: Develop and study algorithms in NLA that use randomization. The idea of introducing randomization to algorithms in NLA has had a profound impact on the efficiency and scale of problems we are able to solve. In my mind, among the key benefits that randomization can bring are the following:

(i) 'Fast+Near-best' instead of 'Slow+best': Classical NLA algorithms are designed (for good reason) to solve problems as accurately as possible. In standard double-precision arithmetic, this means we're aiming for 15 digits of accuracy. In randomized NLA, we often ask for a 'good enough' solution, which might mean we're looking for say 10 digits or even less, which in many cases is more than enough! This flexibility in accuracy can sometimes bring enormous speedups. Randomized SVD is a representative example where this has had a tremendous impact.

(ii) High-probability guarantees rather than worst-case guarantees: Related to (i), classical methods need to solve *all* problems well. The problem is, there are often pathological problems that are exponentially more troublesome than 'average-case' problems; a good example is LU (Gaussian elimination) with partial pivoting, for which the growth factor increases exponentially in the worst case. The key point is, these bad examples are also exponentially rare! Randomization can allow us to turn a pathological problem into an average problem, with high probability; we can thus solve all problems with the speed/reliability of average problems.

(iii) Matrix sketching: The idea of sketching is to reduce the dimension of an enormous matrix A by multiplying a random matrix, say SA. The key insight is that, if A has a certain low-dimensional structure (e.g. low-rank or sparsity), the sketch SA can be shown to retain enough information to solve problems in terms of A. Sketching is a fundamental tool in RNLA, and has been applied to low-rank approximation, least-squares, rank estimation, and recently to linear systems and eigenvalue problems.

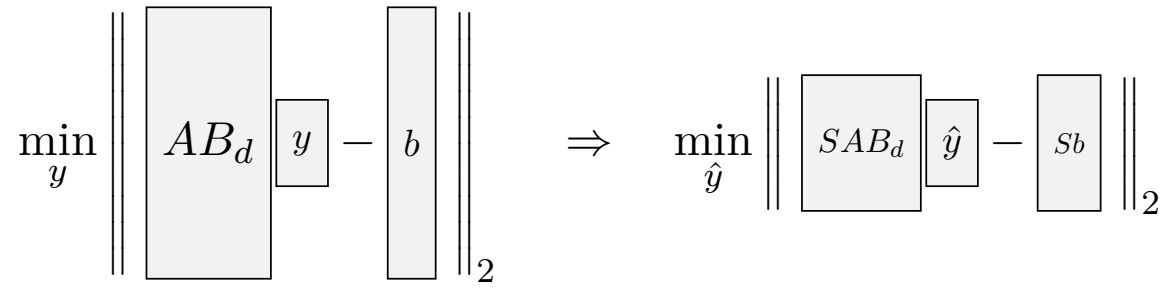
An illustration of a sketch, as appears in a least-squares problem, and a key idea in the sGMRES algorithm; please see preprint with Joel Tropp, also mentioned below.

(iv) Monte-Carlo sampling: Some algorithms in RNLA are based on taking random samples, as in Monte Carlo methods. This allows us to give a (very) rough estimate for the quantity of interest very quickly, usually with significantly lower complexity than a classical approach. A good example is trace estimation. Significant research is currently going into improving and understanding the quality of estimates one can obtain this way.

Of course, there are obvious drawbacks to using randomization: the solution changes every time the algorithm is run! However, I think it is hard to argue against an algorithm that produces solutions that are at least 10-digit accurate with probability say 1-10^{-50}. If you're still worried about the failure probability, a quote from J. H. Wilkinson might help: 'Anyone that unlucky has already been run over by a bus!'

My work in RNLA include

Fast & Accurate Randomized Algorithms for Linear Systems and Eigenvalue Problems (with Joel A.Tropp), Preprint. Introduces randomized algorithms for linear systems and eigenvalue problems. The idea is simple, use sketching in classical NLA iterative algorithms. It can result in significant speedup.

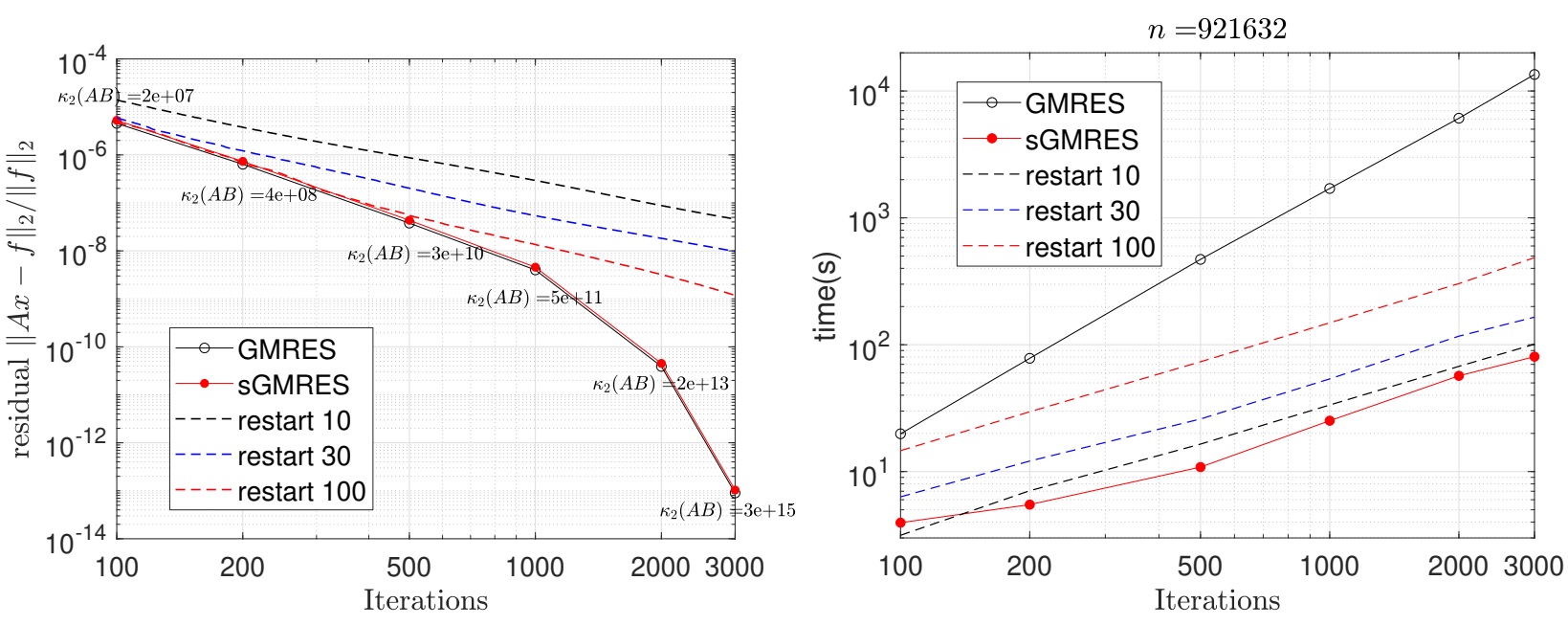
The figure above is a highlight from the paper, where we achieve ~100x speedup over GMRES for solving a linear system.

Fast and stable randomized low-rank matrix approximation, Preprint. Study of a fast low-rank approximation algorithm, and in particular its numerical stability, which is an important aspect in RNLA that is often left unexplored.

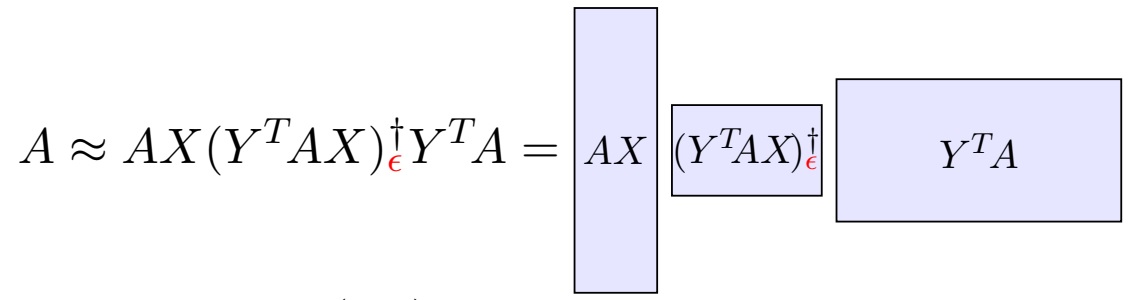
The paper shows this approximation (where X,Y are random sketch matrices) has a near-optimal approximation, and that it can be implemented in a numerically stable fashion.

Fast randomized numerical rank estimation (with Maike Meier), Preprint. Studies a fast and practical algorithm for estimating the numerical rank of a matrix using sketching. (Maike is my Dphil student and this is our first paper!)

Randomized low-rank approximation for symmetric indefinite matrices (with Taejun Park), Preprint. Introduces a variant of Nystrom's method (a fast algorithm for approximating positive semidefinite matrices) that can be applied even when the matrix has negative eigenvalues. (Taejun is also my Dphil student!)

Computing with rational functions

I am also very interested in computing with rational functions, and devising efficient algorithms based on rational approximation. Approximation theory underlies much (most) of computational mathematics---as we almost always solve problems for which the exact solution is uncomputable, we have to approximate the solution. This is where approximation theory comes in---to understand the accuracy and convergence of numerical algorithms, we almost invariably draw from tools in approximation theory. Finding solutions to (continuous) problems in scientific computing with guaranteed accuracy and lightning speed is in my mind the main goal of numerical analysis.

Naturally, approximation using polynomials has long been the classical and central topic in approximation theory. Nonetheless, there are compelling reasons to use rational functions instead of polynomials. First, there are functions to which rational functions converge almost exponentially, whereas polynomials only converge algebraically, or even not converge at all. I have been intrigued by the ability of rational functions to solve difficult problems with exceptional speed. Indeed many algorithms can (and should!) be understood from the viewpoint of rational approximation; these include the QR algorithm, most algorithms for matrix functions, and many (most) algorithms that use Newton's method.

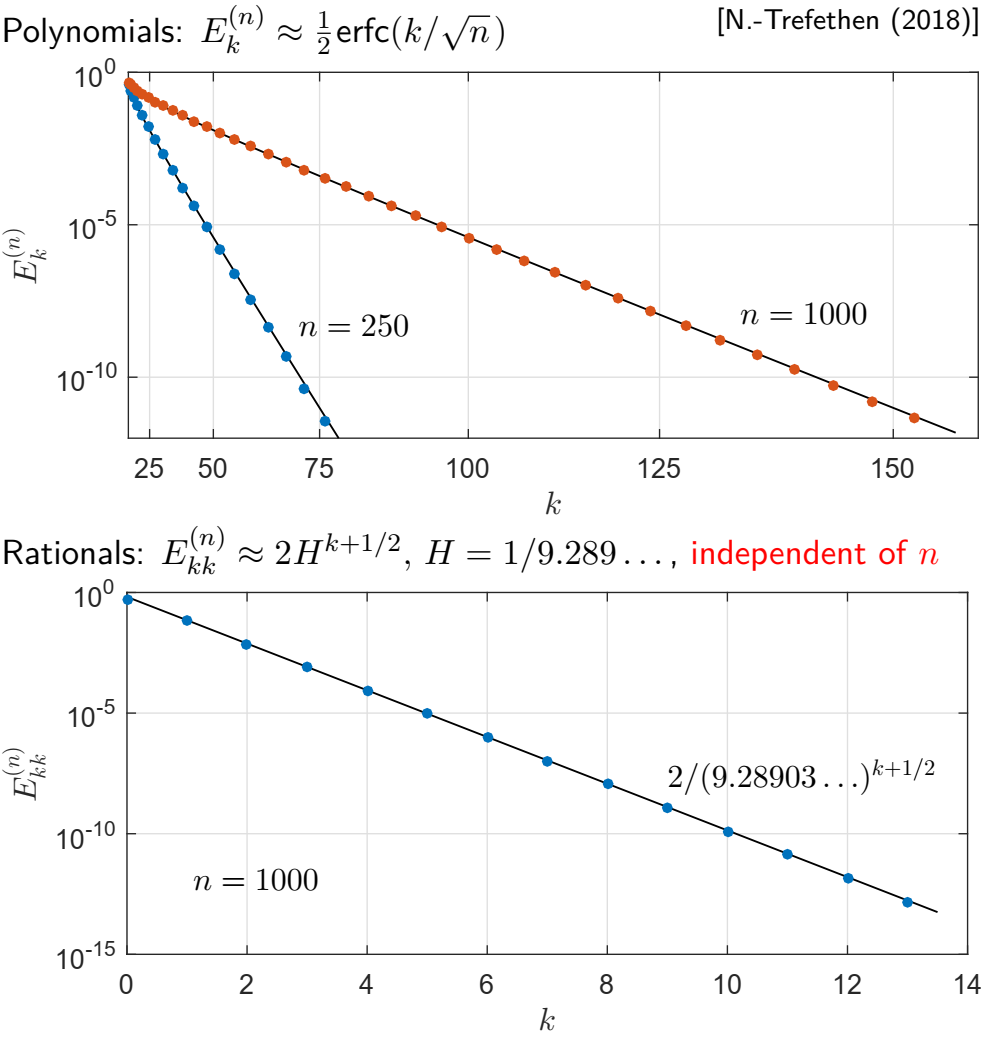
This figure illustrates a result in this paper, which shows that rational functions can approximate x^n with exponential accuracy, regardless of n. By contrast, polynomials need degree ~sqrt(n) to get anywhere. The computation is done using the minimax algorithm developed here.

The AAA algorithm: This is a very versatile and reliable algorithm for computing a rational approximation to a given univariate (real or complex) function. It has been applied successfuly to solve a number of problems; see e.g. Nick Trefethen's talk here. Please try it out if you want to approximate a (unknown) function by a rational function! Click here for the paper. It is implemented in Chebfun; which is a remarkable MATLAB toolbox that allows one to do all sorts of computation with polynomials and rational functions; I suggest you try it out if you haven't already!

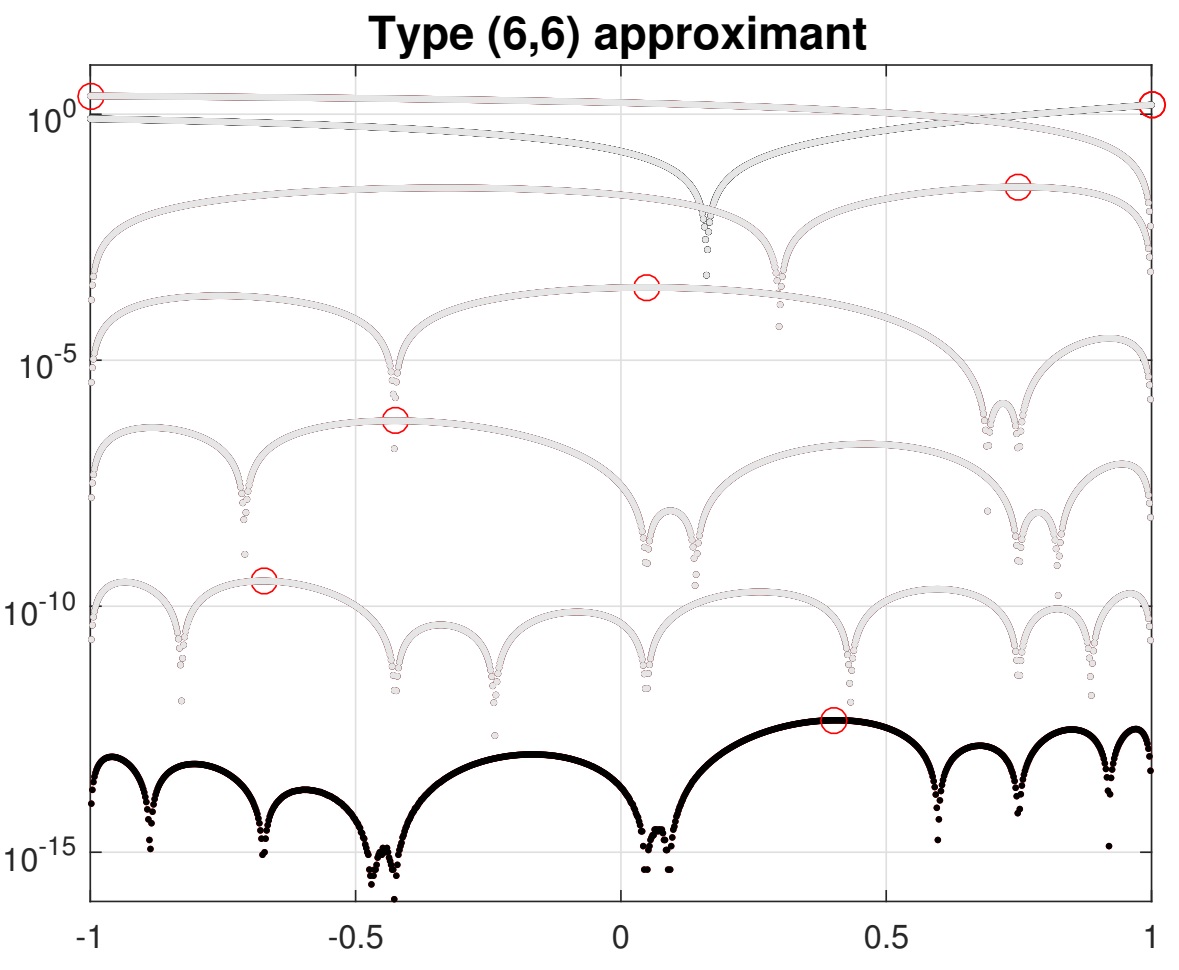
This illustrates the workings of the AAA algorithm. It chooses an interpolation point in a greedy fashion, while using the other (half) degrees of freedom to do a linearized least-squares fitting of the sampled data. The red points are the location of the maximum error in the previous iteration, which is then taken to be the interpolation point in the next iteration (so the error there becomes 0).
Here AAA is used to approximate a transfer function arising in model order reduction.

Besides AAA, I've used rational functions in devising algorithms for the SVD, 'rationalized' neural networks (which so far had small impact but I think they might in future!) PDE solver, and their theoretical properties, e.g. this cute paper.

Classical topics in NLA and related fields

Besides RNLA and rational approximation, I am actively interested in any of the topics below.

Statistics and linear algebra. I have a growing interest in the intersection of statistics(+probability, data science) and linear algebra and approximation theory. I believe there is significant scope for interesting work here. In particular, Monte Carlo methods can be understood from an approximation+LA viewpoint, and there is much to contribute to the theory and practice in PCA from an NLA viewpoint.

Perturbation theory and matrix analysis. This has long been my fascination; indeed it was the first topic that got me into NLA. Matrix perturbation theory studies the behavior of matrix properties (e.g. eigenvalues, singular values) under perturbation. This might sound academic or niche, but perturbation theory can give insight into e.g. the difficulty/sensitivity of problems, or help us understand why certain algorithms work, or don't work. Despite its long history, I think there are a large number of problems in perturbation theory and matrix analysis that should be worked out, many inspired by RNLA. Among my favorite papers in this direction are one on eigenvector perturbation theory,

Classical (dense) algorithms in NLA. I have long worked on NLA algorithms for solving problems with dense matrices, including the SVD, eigenvalue problems, and matrix decompositions. While these are classical problems for which exceptionally reliable algorithms are available, there are often opportunities to improve them further: for example inspired by today's computational architecture, or by taking advantage of tools from other fields, e.g. approximation theory or optimization (or even deep learning---there's a fascinating recent article that identified a fast way to multiply matrices using deep learning). Moreover, their stability analysis is often still an open problem.

Optimization. I was part of an optimization group while at the University of Tokyo. Of particular interest to me is (i) solving optimization problems that are non-convex by reducing them to eigenvalue problems, and (ii) using randomization for solving optimization problems.

In addition, while I can hardly call myself an expert, fields I have had the opportunity to work in (due largely to collaborators with serious expertise) include compressed sensing, tensors, preconditioning, differential equations, quantum computing, signal processing, and deep learning. Linear algebra and/or approximation theory play a (perhaps hidden but) important role in all of these, and techniques and theory in (R)NLA can make a (often substantial) difference. I believe in the universal and eternal importance of NLA in computational mathematics.