For my DPhil thesis, we partnered with Nestlé to better understand a manufacturing process known as extrusion. This process involves forcing a mixture containing a volatile component through a small die. This results in a significant pressure drop in the mixture, and subsequent vapourisation of the volatile component. The resulting flow contains two phases, and expands rapidly upon meeting the atmosphere outside the die. This exsolution and expansion stage of extrusion is known as the flash, and, due to the plethora of interesting modelling and mathematical challenges it presents, is the part of extrusion we are particularly interested in.
The equations governing the behaviour of the mixture being extruded are complicated. We are also faced with tricky boundary conditions including: a free boundary, and a change from no-slip conditions to those of a free-boundary. We tackle these challenges by refining the questions we ask of the system. In doing so, we instead look for particular features of the solutions, and we are able to reduce the complexity of the system. For example, we are interested in how the shape of the product evolves after meeting the atmosphere, and how the texture of the product depends on the extruder setup.
If we are only interested in understanding the shape the product takes, we can make a number of sensible assumptions, and consider a reduced set of equations that capture this evolution. This reduced system couples a two-dimensional (2D) model for cross-sectional change (see fig. 1) to a one-dimensional (1D) model for axial-variation. The result is a three-dimensional (3D) surface illustrating the evolution of the product's shape (see fig. 2).
We can better understand the texture of the product, for which the final volume-fraction of gas is used as a proxy, by considering special (simple) die geometries. For example, for an axisymmetric system we can apply a coordinate transformation that maps our free-boundary problem to a fixed, rectangular domain. Eliminating the free-boundary component of the problem, in exchange for increasing the complexity of the governing equations, eliminates many of the computational challenges associated with this problem. As a result we are able to predict variations in gas volume-fraction throughout the product (see fig. 3).
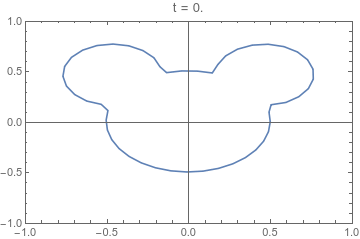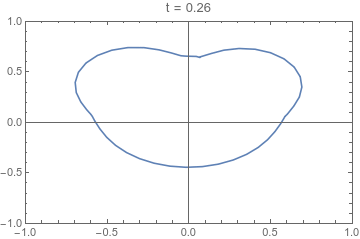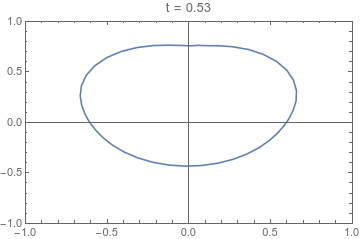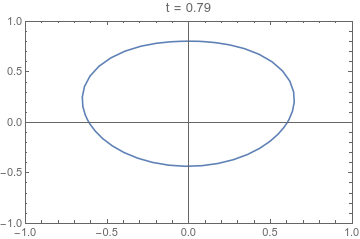
The evolution of a cross-section of an extruded product with respect to a reduced-time variable τ. This 2D model is coupled to a 1D model of axial evolution. Through this coupling, the map from τ to axial distance is determined.

A 3D illustration of the evolution of an extruded mixture. The transition from red to blue colouring indicates the drop in temperature as the product expands.
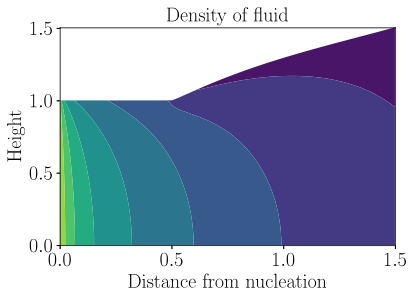
The predicted density field of an extruded mixture. Greener colours indicate higher density, and purple colours indicate lower density.