Symmetry friendship bracelets


All of my bracelets have translational symmetry: they are made up of a pattern that repeats along the length of the bracelet. (For the purposes of mathematics, you should think of these bracelets as infinitely long! And another technical detail: I'm only exploring 'discrete' options, so for example a plain blue bracelet wouldn't count because any translation would be a symmetry.) Then there are a few other types of symmetry that each might have.
- It might have a line of symmetry along the length of the bracelet (I call this 'horizontal symmetry').
- It might have (repeated) lines of symmetry across the width of the bracelet (I call this 'vertical symmetry').
- It might have rotational symmetry, under rotations by 180 degrees about suitable (repeated) points.
- It might have glide symmetry: reflect in a line along the length of the bracelet, and also translate.
Some of these types of symmetry are interconnected: if you have one or two, then you might automatically have another. For example, a bracelet with horizontal symmetry must also have glide symmetry. It turns out that there are seven possible types of symmetry pattern (combinations of the above types of symmetry) that such a bracelet can have. Each corresponds to what's called a frieze group - there are seven types of frieze group.
Below are photos of bracelets illustrating the seven types of symmetry (in some cases I made more than one bracelet with the same symmetry type), as well as designs you can use if you'd like to make your own. You can use whatever colours you like - but watch out, sometimes you can change the type of symmetry by changing the colours! I encourage you to make your own designs. You could make a design and then decide what symmetry type is has, or (harder) pick a type of symmetry and try to produce a design with that symmetry type! I found it helpful to print off some squared paper to make my designs.
To make your own friendship bracelet, you can use any type of yarn, thread or string you have. Most of my examples below use Aran weight knitting yarn, but some use stranded cotton (using all six strands together). You'll need to learn two types of knot: the left-over-right, and the right-over-left. If the diagram shows left-over-right, then you make two left-over-right knots of the type shown here for that cross. If the diagram shows right-over-left, then you make two right-over-left knots. In a few diagrams, you'll find the two threads don't cross at all, but instead 'bounce' off each other, so you do one knot of each type - you'll figure it out! You'll want to fix the knot at the top of your bracelet. I used a clipboard, but you could also tape it to a table, pin it to something - anything that you can gently pull against. You can search online for lots of guides, pictures and videos to help you learn to make friendship bracelets.


Type 1 - no extra symmetry


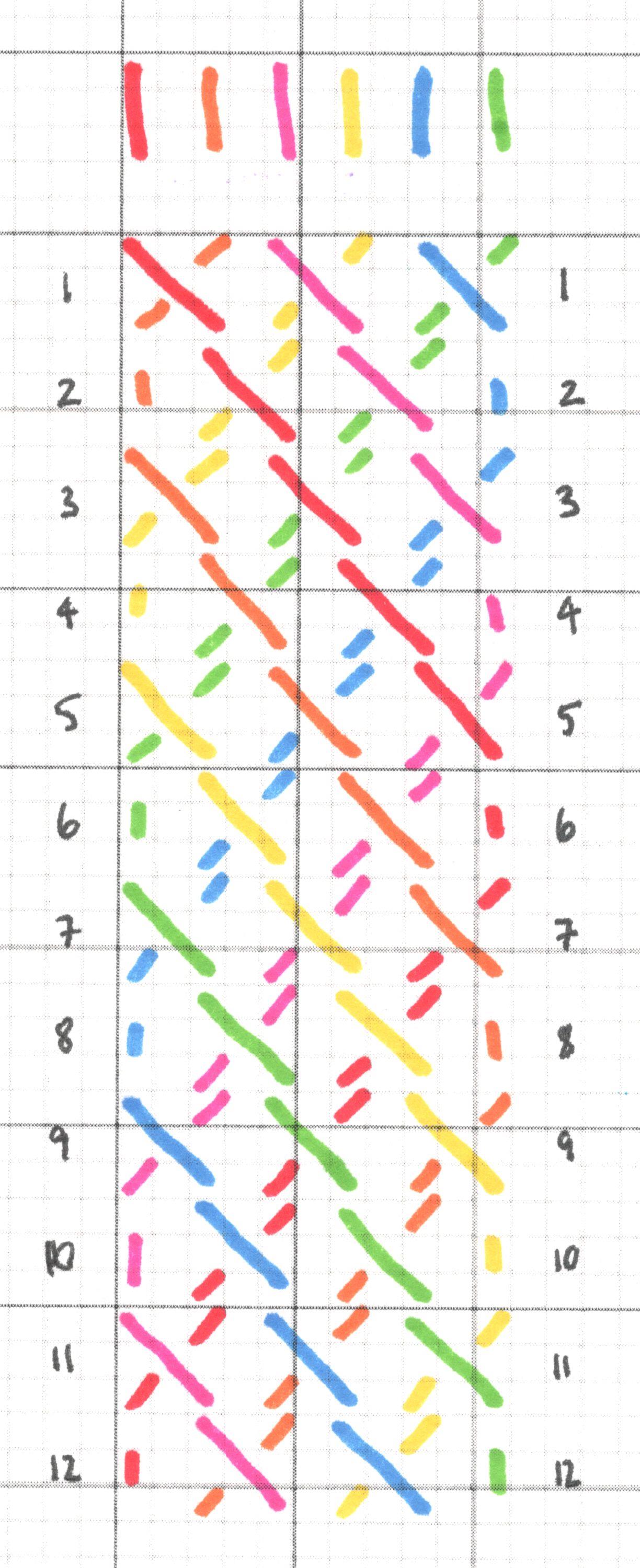
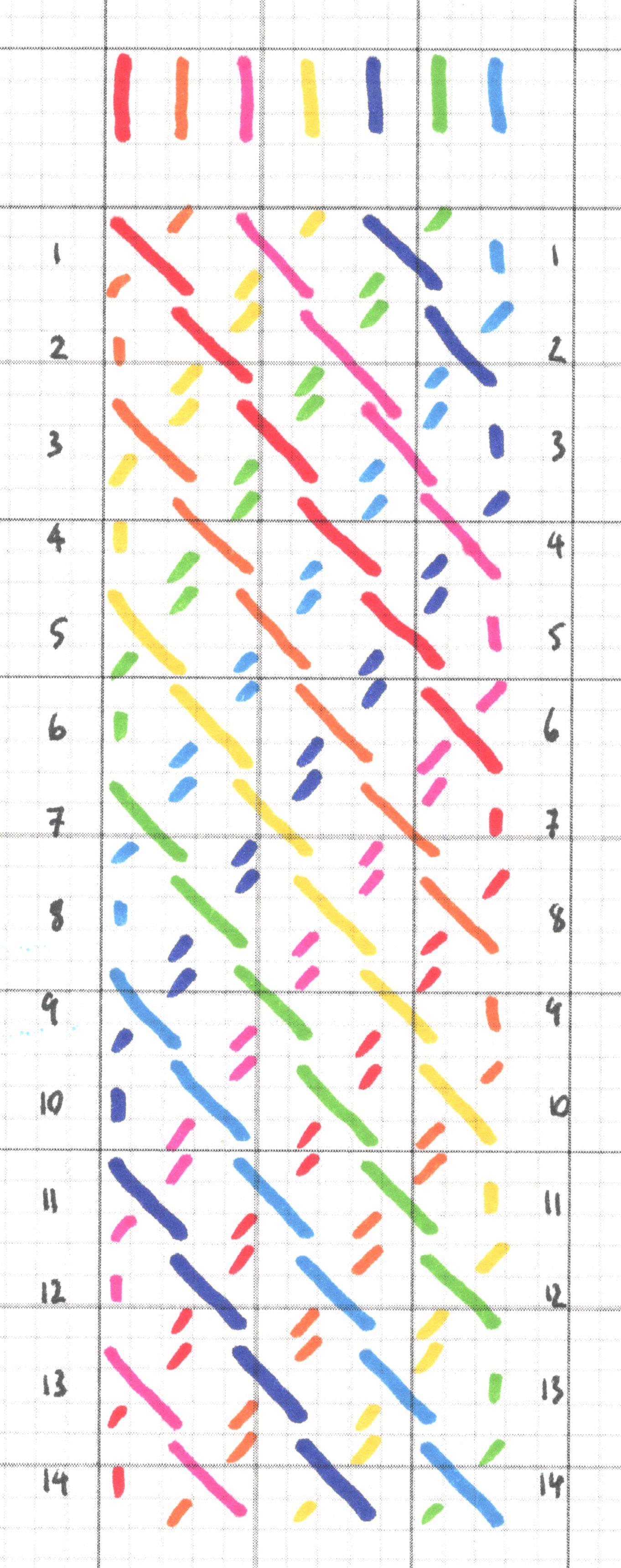
Type 2 - glide symmetry



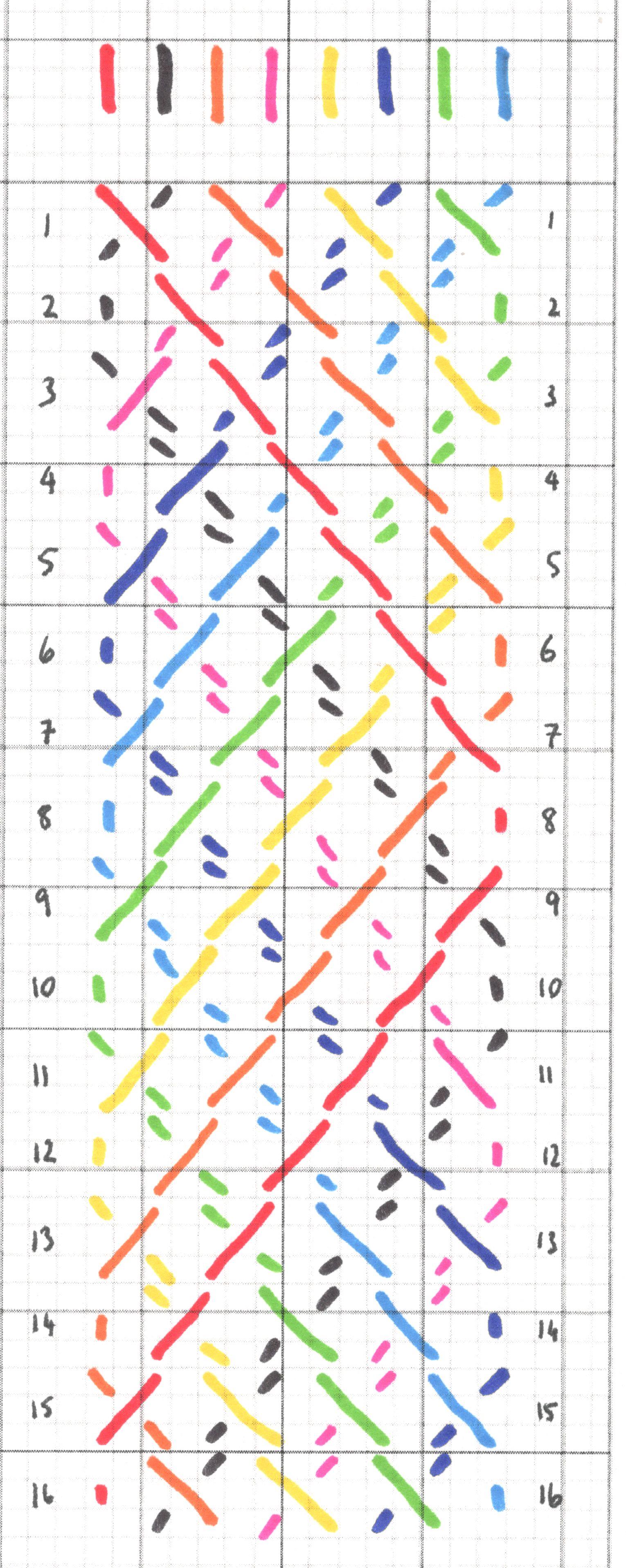
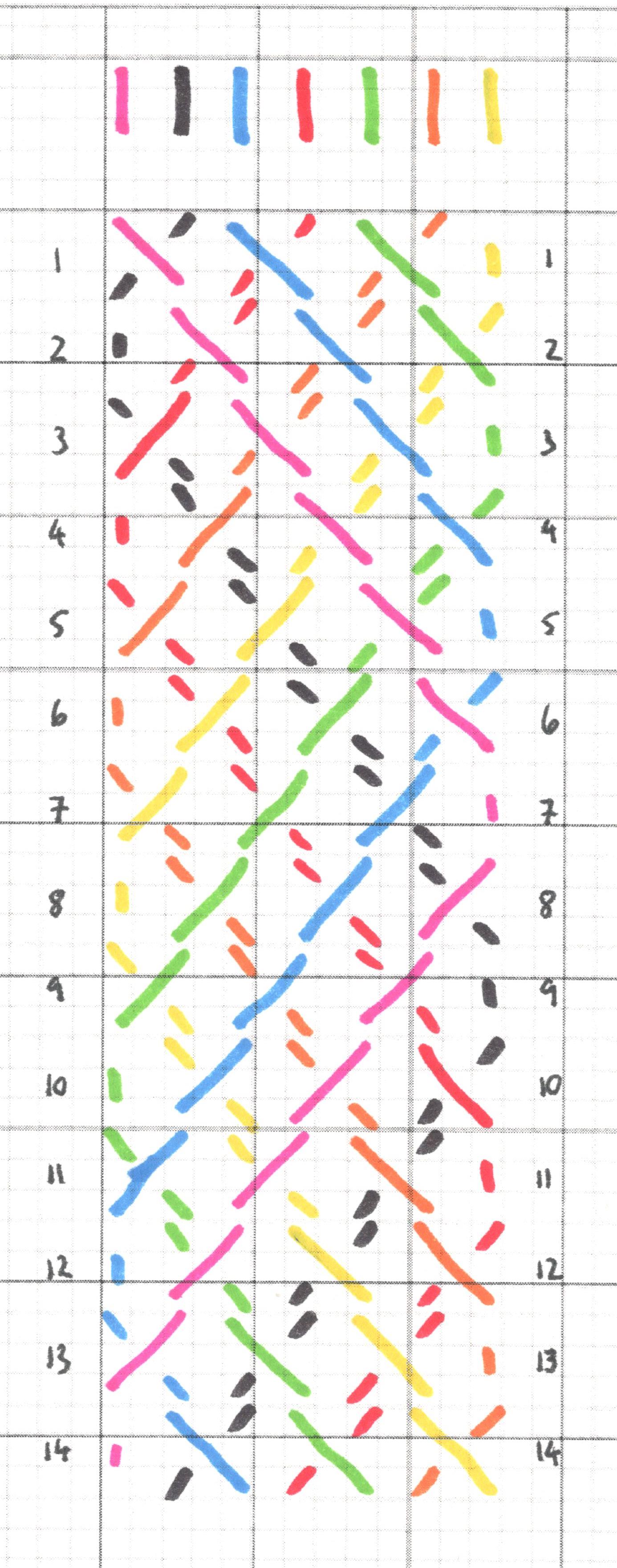
Type 3 - vertical symmetry

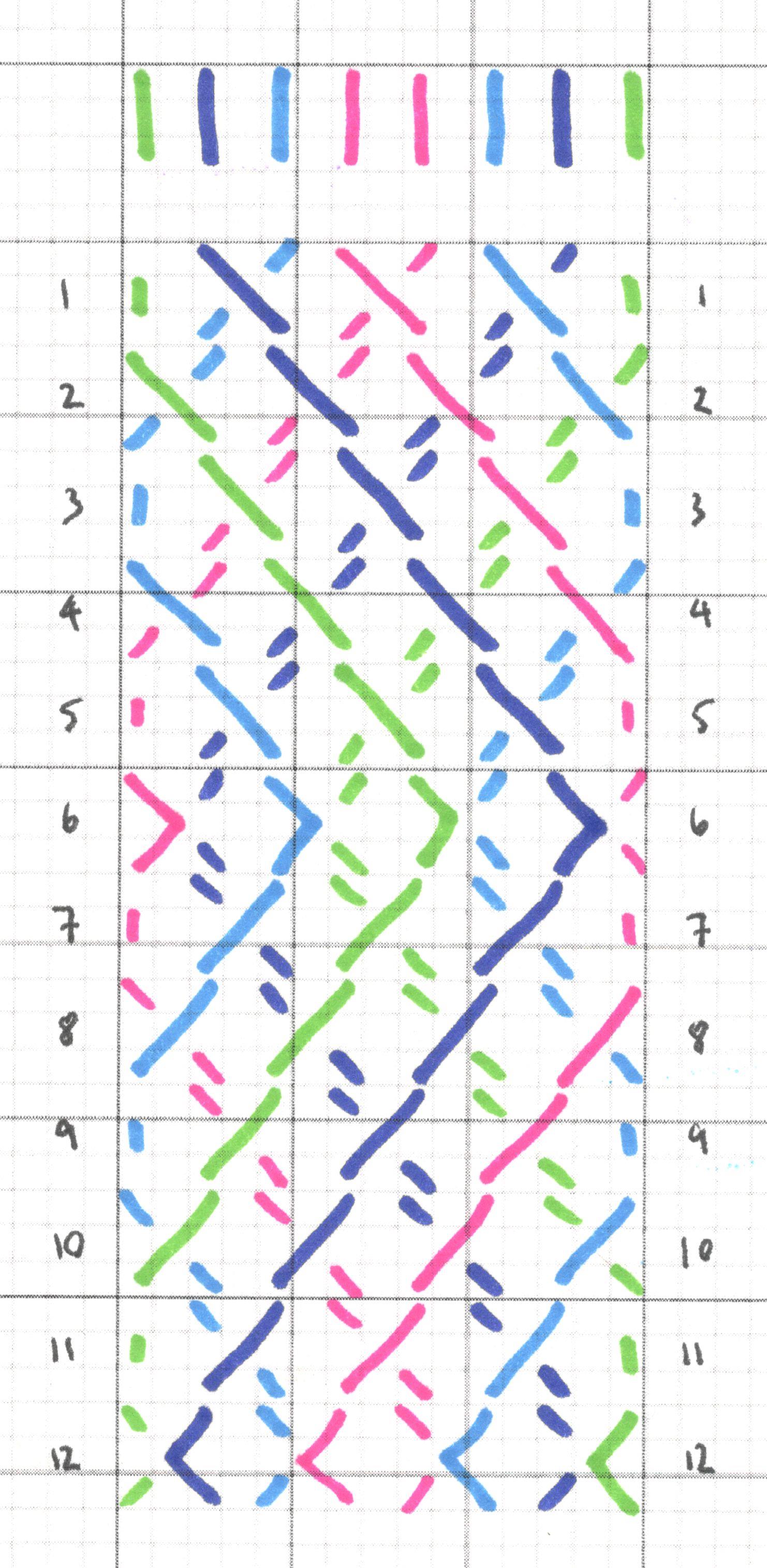
Type 4 - rotational symmetry

Type 5 - glide, rotational and vertical symmetry

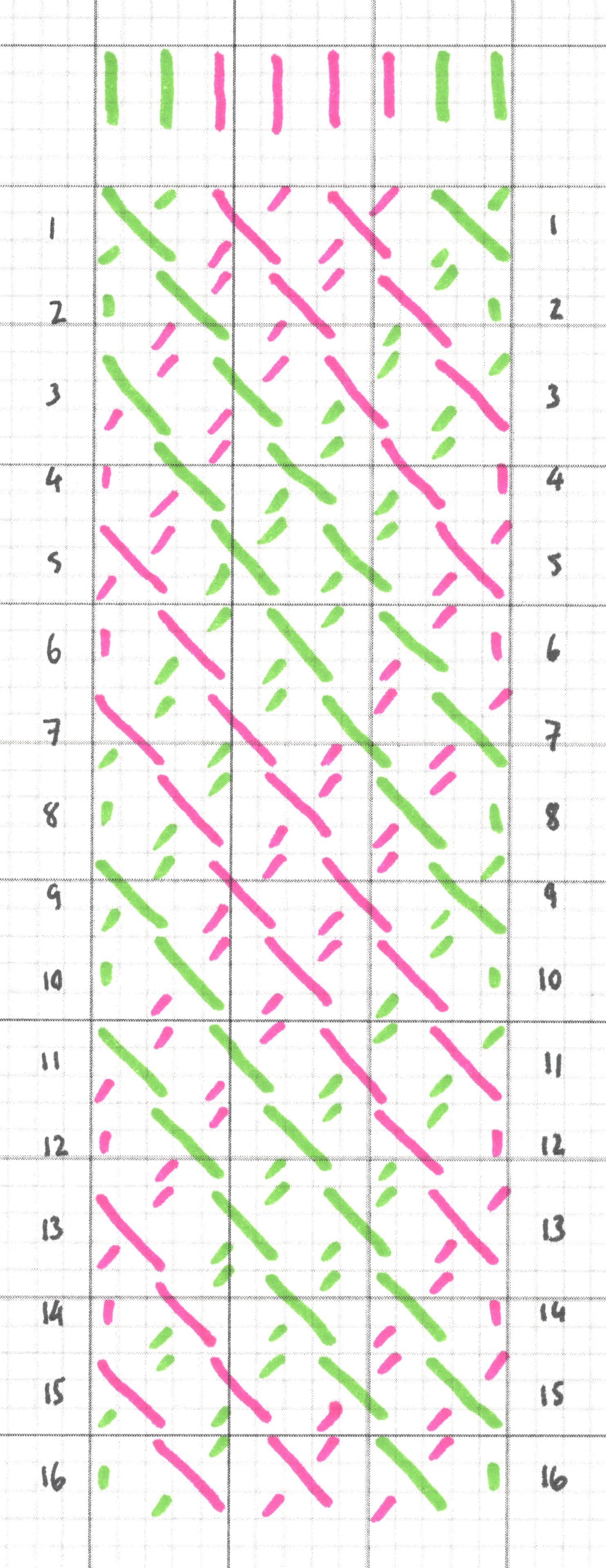
Type 6 - horizontal and glide symmetry


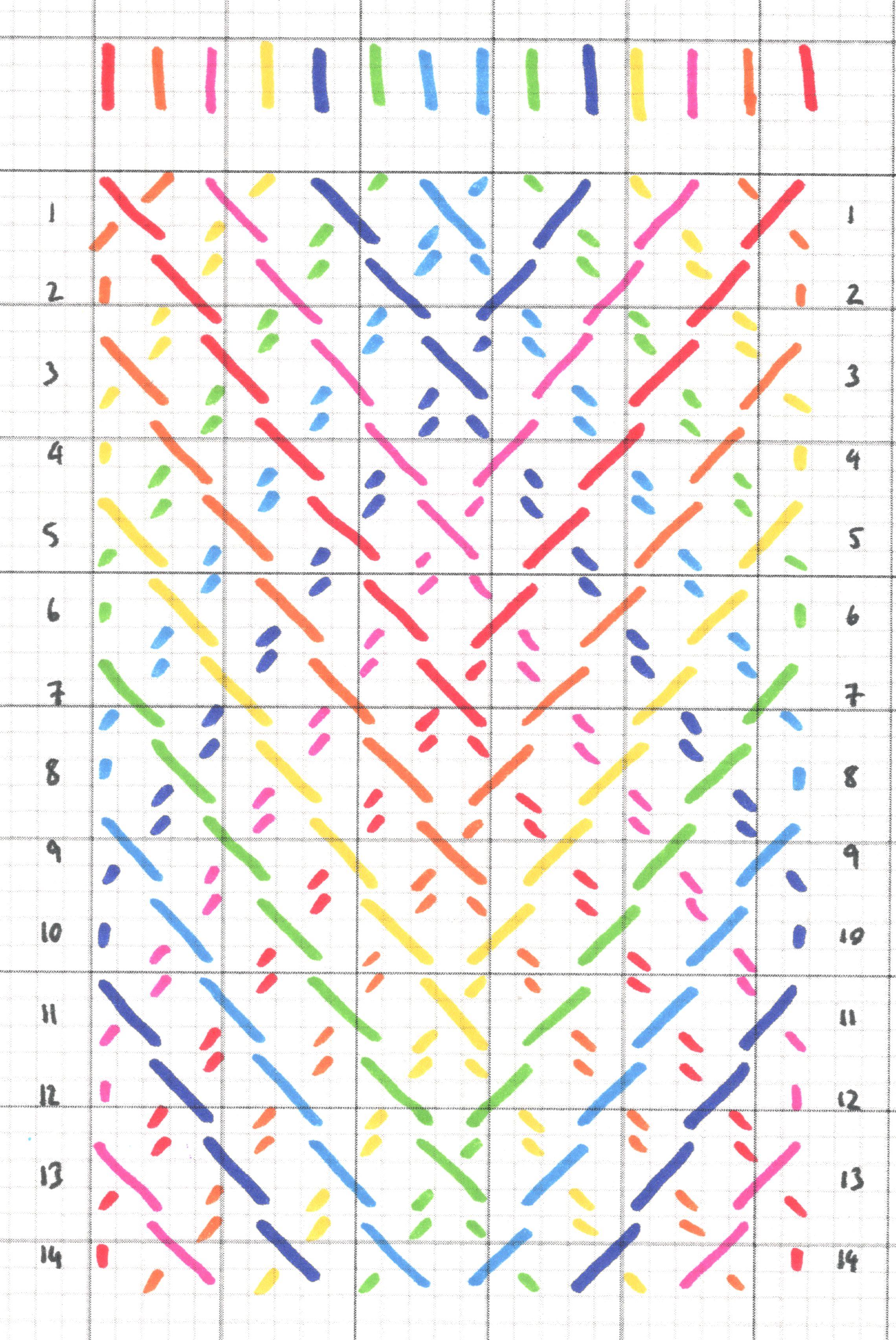
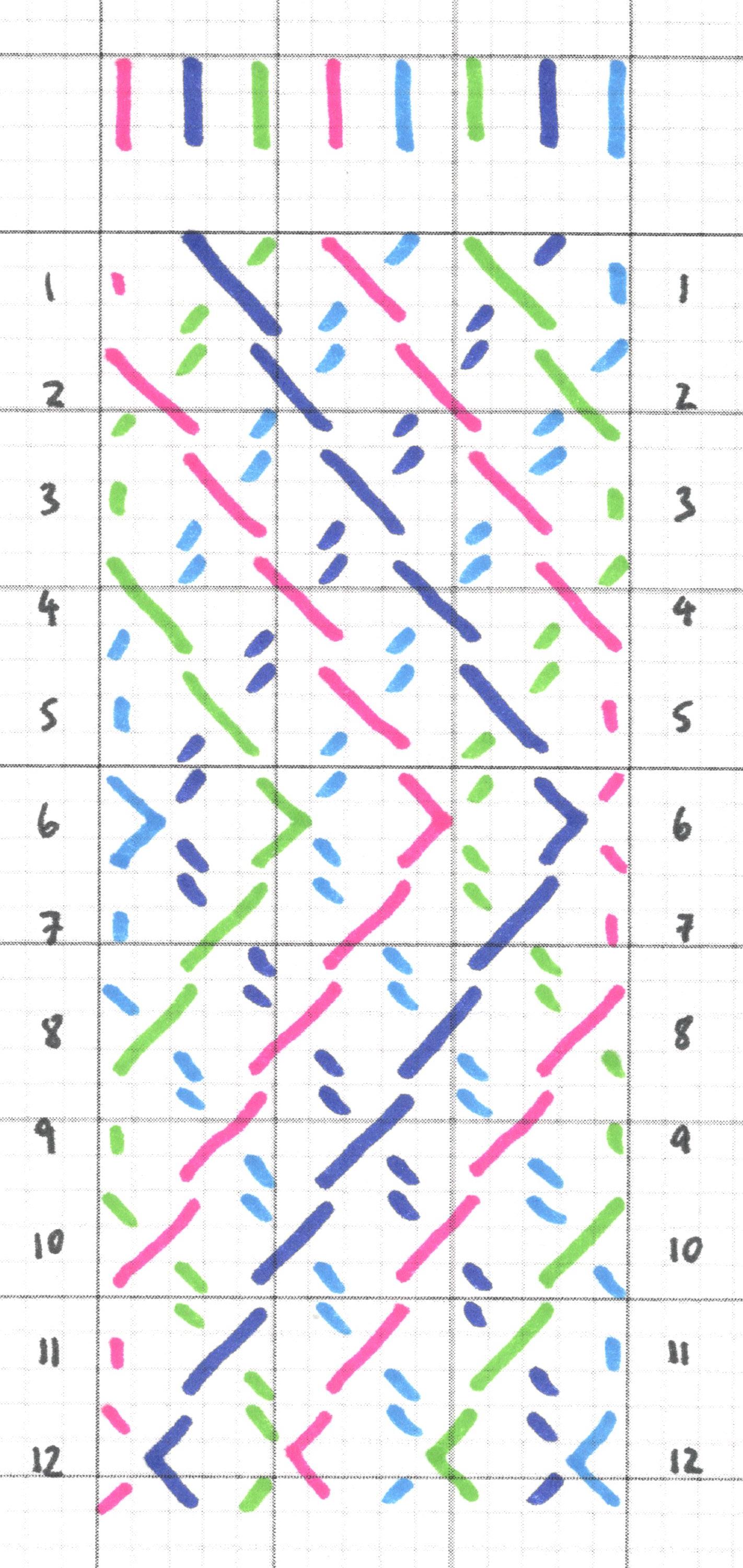
Type 7 - glide, horizontal, rotational and vertical symmetry

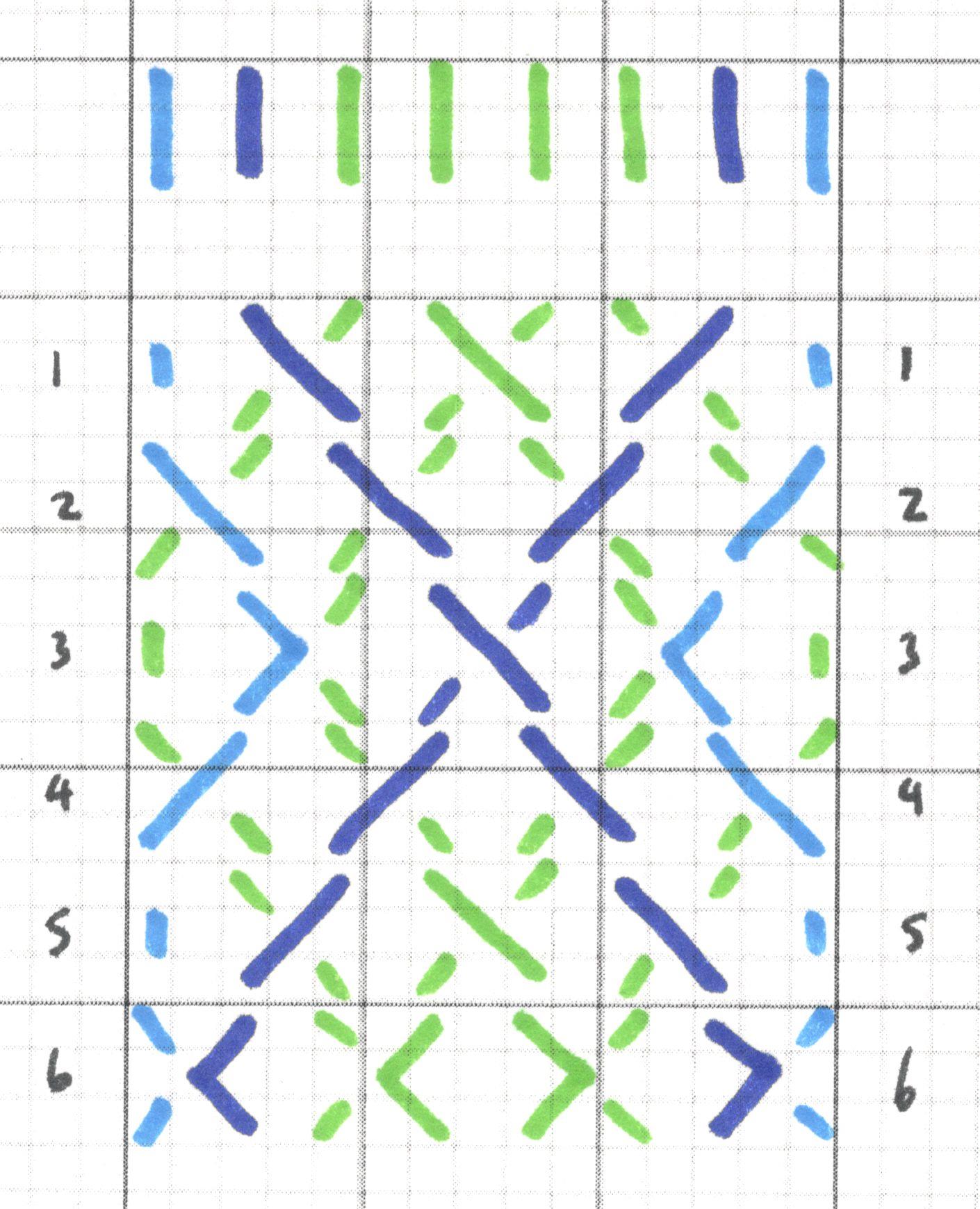
Symmetry scarves
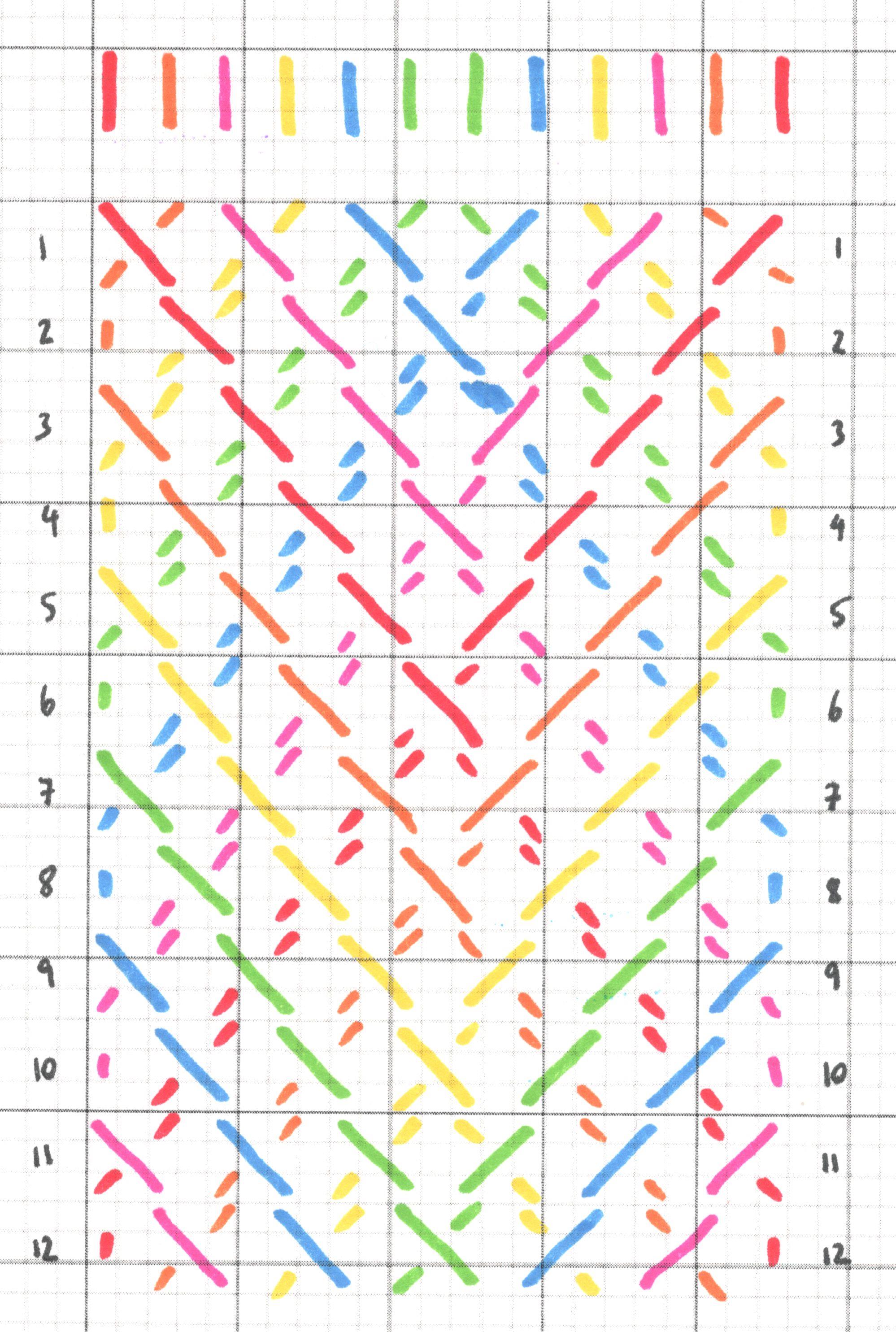
I've been exploring the same maths of symmetry types (frieze groups) through knitted scarves too. Since there are seven symmetry types, I thought I'd make a rainbow of scarves. Each has a white crochet border, to help it uncurl, and you can see that (and the pins I used to hold the scarves in place!) in some of the photos. For each scarf, there's a photo showing most of its length for the overall effect, and a close up showing the design. I've also provided the patterns I used, just in case anyone fancies knitting their own.
The scarves are shown in rainbow order here. Using the numbering of types of symmetry pattern from the bracelets section above, they go in reverse order, from red (type 7) to violet (type 1).














Patterns (all png files). For two of them I couldn't find the symbols I wanted on the software, so there are blanks in the main version, and a second version where I've drawn on the symbols by hand. Hopefully between the two versions you can find what you want!
- Red scarf
- Orange scarf
- Yellow scarf and Yellow scarf with handwritten annotation
- Green scarf
- Blue scarf
- Indigo scarf
- Violet scarf and Violet scarf with handwritten annotation
This page last updated 2 June 2021.