
Current: Announcements and imminent deadlines
To my students: still lurking here? The class is over, but you can peruse the course evaluations. And you can also try to locate yourself in this video from the last day of our class (Wednesday April 30th, 2014): what we do in this life echoes on YouTube.
To other students: you must be cramming for an upcoming exam. First cut your teeth on the material from the "Assignments: homework and practice problems" area and use the HW solutions only if necessary. Once you're confident, go straight to the "Archive: Exams and Solutions" tab. My students had 50 minutes for each midterm, but you should really try to get each exam done within 40 minutes (all at once, no snack breaks!). Textbooks and calculators were neither necessary nor allowed. All the best!
To instructors: perhaps you're looking to organize your own course (or maybe a single lecture). In the "Material: textbooks and lecture notes" section you can find hand-written and scanned friendly notes which I used for each class. If I were teaching the course again, I would almost certainly move Lecture 11 (on graphs and adjacency matrices) to later in the semester and Lecture 29 (on Jordan Forms) to earlier. Good luck!
Assignments: Homeworks and practice problems
Homework 1 was collected on Friday 1/31. Here are Hua's solutions.
Homework 2 was collected on Monday 2/10. Here are Hua's solutions.
Homework 3 was collected on Monday 2/24. Here are Hua's solutions.
Homework 4 was collected on Wednesday 3/19. Here are Hua's solutions.
Homework 5 was collected on Wednesday 3/26. Here are Hua's solutions.
Homework 6 was collected on Wednesday 4/09 (due date extended from Monday 4/07!).
Homework 7 was collected on Friday 4/25.
Homework 8 will not be collected: it is meant for Final Exam practice.
Practice problems 1 for the first midterm, courtesy of Hua. See also Quizzes 1 and 2 on Hua's class page.. Finally, most problems in Dr. Kazdan's first midterm from Spring 2013 (see here) should be accessible. His exam uses the terms Kernel for null space and Image for column space.
The official prerequisite for this class is an introductory linear algebra course, which corresponds to Math 240 at Penn. Fortunately for you, this prerequisite is not being strictly enforced. Unfortunately for you, I might assume that you know this stuff. The best way to see whether you are ready for Math 312 involves trying as many old final exam problems from Math 240 as possible. If you can solve most of them correctly, you are ready. Otherwise, you will need to work extra-hard during the first few weeks of class.
Logistics: Location, schedule and grading
Location: We will meet every Monday, Wednesday and Friday from 11 AM to 12 PM in Room A4 of the DRL building.
Our Schedule, being somewhat more flexible than our location, will remain in flux until I can assess your backgrounds and interests. The basic idea is to divide this semester into three units: the first unit will deal with the algebra, geometry and mechanics underlying matrix-vector operations. The second unit will involve eigen-decomposition of square matrices. In the third unit, we will investigate several important advanced topics. In particular, we will survey modern applications of linear algebra to ranking, image compression and so forth.
Our Grading scheme's simplicity is exceeded only by its deviousness. You can find your individual grades on this class's Canvas page. This is how you will be graded:
| Regular Homework Assigments | 20% |
| Two In-Class Midterms | 40% |
| Giant Final of Doom | 40% |
The grades were submitted to the registrar on Friday the 9th of May. Here's a graph (no, not the kind with nodes and edges) illustrating class performance:
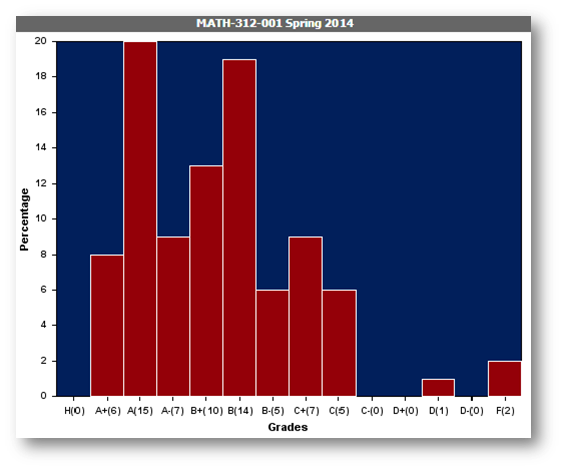
Regardless of how you feel about your grade, or what you will retain in the years (months? days??) to come, you should keep in mind that the material which we have covered -- specially near the end -- is quite hard-core and current. As I've mentioned before, Perron-Frobenius theory underlies almost all modern search engine algorithms. SVDs are used regularly for image-compression. Billions of dollars are being funneled into research which hopes to produce even faster Fourier transforms. Entire books are dedicated to the manifold applications of linear optimization in Economics. You've seen some things this semester. And hopefully, they've seen you too.
Material: Textbooks and lecture notes
Some homework problems will be chosen from our main textbook Introduction to Linear Algebra by Gilbert Strang (4th Ed) available here and also at the Penn bookstore. Your homework assignments will consist of full problems (rather than numbers, eg, there will be no "turn in numbers 3, 12 and 22 from Section 2.2), so you don't need a copy of this book to access your homework. Ever.
As a Reference text, I'd recommend the example-filled book by David Poole called Linear Algebra: a Modern Introduction available here. Yes, it's rather expensive. No, you don't have to buy it. I have a copy and I kind of like it, so I might use parts of it to prepare some of the later lectures which concentrate around applications. A free online textbook which takes a slightly more abstract approach than our class is Linear Algebra Done Wrong by Sergei Treil. The pdf can be directly accessed by clicking here. I strongly urge you to not judge this book by its title!
Occasionally, I will put up scanned versions of hand-written notes which I use for lecturing. You may (and should!) use these notes as an outline for reviewing the material.
Lecture 1: The Algebra and Geometry of Linear Equations.
Lecture 2: Counting Solutions of Linear Systems.
Lecture 3: Enter the Matrix.
Lecture 4: Understanding Inverses.
Lecture 5: What does my Matrix do?
Lecture 6: Linear combinations and Vector spaces.
Lecture 7: Null space, Column space and Dimension-counting.
Lecture 8: Linear Independence, Spans and Basis.
Lecture 9: The Fundamental Theorem of Linear Algebra.
Lecture 10: Understanding the Four Fundamental Spaces.
Lecture 11: Graphs and their Adjacency Matrices.
Lecture 12: Orthogonality.
Lecture 13: Projections.
Lecture 14: Least Squares.
Lecture 15: Orthogonal Matrices and Gram-Schmidt.
Lecture 16: Determinants.
Lecture 17: More Determinants.
Lecture 18: Eigenstuff.
Lecture 19: Diagonalization.
Lecture 20: Linear Differential Systems.
Lecture 21: The Spectral Theorem.
Lecture 22: The Singular Value Decomposition.
Lecture 23: Markov Chains.
Lecture 24: The Perron-Frobenius Theorem.
Lecture 25: Linear Programming.
Lecture 26: The Simplex Method.
Lecture 27: The Fourier Transform.
Lecture 28: The Fast Fourier Transform.
Lecture 29: The Jordan Form.
Archive: Exams and solutions
The first exam was held in class on Wednesday, February 19th. Here you can find its solutions as well as a grading rubric.
The second exam was given on Wednesday, April 2nd. Here are the solutions and the rubric which guided the grading process.
See also Dr. Jerry Kazdan's exam material from Spring 2013 located at the bottom of this webpage.
Instructors: Contact information, office hours

My name is Vidit Nanda, and I'm a post-doc here at Penn. The easiest way to get in touch with me is via email to vnanda at sas dot upenn dot edu. Please be sure to include "Math 312" in the email title, otherwise I may not see your message. Often, you can also find me in room 3C5 on the third floor of DRL. Since DRL is the labyrinth where we meet for class, you don't have to walk too far to reach my office (provided, of course, that you don't get lost en route).
My office hours for Spring 2014 are Monday 12pm - 1pm and also Wednesday 3pm - 4pm. If these times are unsuitable, you can always email me on a case-by-case basis and set up an appointment. You might also want to visit Hua during his office hours (see below).
This is the first time I'm teaching at Penn, but I've taught multivariable calculus several times while I was a graduate student at Rutgers. You can see what my students had to say about me here.

The TA for our course is Hua Qiang and he can be reached by email to huaqiang at math dot upenn dot edu. His office hours are Tuesday and Thursday 4:30pm - 5:30pm or by appointment in Room 4C13 on the fourth floor of the DRL building. Hua has also prepared this webpage for our class. On that page he will post homework solutions (after the due dates, of course).
Resources: Additional help and useful links
Come to class, ask questions fearlessly during lectures, and please don't hesitate to send me email or come to my office hours whenever you feel stuck on a problem or confused by a concept. If you need help with studying or problem-solving outside of class and office hours, you can find official Penn tutoring here. If you find yourself struggling, it is better to seek help sooner rather than later.