I am an applied mathematician, interested in mathematical modelling and applying computational, analytical and occasionally experimental tools to answer questions in the natural sciences, especially the biological world. My work is focussed primarily on the continuum scale, in particular I am interested in: mechanical biology and physiology, growth and pattern formation, morphoelasticity, and elastic mechanisms in nature. Earlier work involved ferrohydrodynamics, minimal surfaces, and electrostatics.
Growth is the process by which a material gains mass. It is ubiquitous in nature, common in some form to all living entities, and found in many industrial applications and physical phenomena as well. It is the process that links the graceful neck of the giraffe to the powerful horns of the ram to the formation of a planet as a dust cloud collapses under gravity. In biological tissues, such as arteries, skin tissues, airways, and plants, growth is a complex process, which can be analysed from multiple perspectives (biological, chemical, evolutionary, ...) as well as on multiple length and time scales.
My interest is on the mechanics of growth processes, and understanding the form of biological structures through analysis of the physical forces underlying their morphogenesis.
Seashells have intrigued scientists for centuries, often forming a paradigm for evolutionary theories. Yet the developmental mechanisms underlying shell formation are largely not understood. We have developed a general model for shell growth based entirely on the local shell geometry and mechanical interactions between the rigid shell aperture, where shell growth occurs, and the mollusc, the creature that lives in and builds the shell.
Pictured: Left: We have uncovered a natural mechanism to explain the formation of spines in certain molluscs. Right: Ammonites are an iconic group of Cephalopods that have been extinct for over 100 million years yet are still of great interest to paleontologists. Our modelling framework has provided the first quantitative explanation for the formation of the ribbing pattern on these beautiful shells.
The plant world presents us with a fascinating and beautiful diversity of complex patterns and functions. How do plants grow to form such intricate patterns? How does form lead to function? These are some of the questions I seek to answer. While we often think of plants as being completely stationary, they are anything but, often achieving large scale motion through clever manipulations of geometry and mechanics. One particularly interesting class of such motions is called tropism, which generally describes the movement of a plant in response to a stimulus. Documented since the time of Darwin, tropisms are ubiquitous in the plant world, and can consist of a growth response to many different types of stimulus, for example a sunflower bending towards the light of the sun, or a potted plant set on its side curving upward to align with gravity. Tropic growth is a process that involves the coordination of activities across multiple length scales. We have developed a mathematical framework for modelling tropic plant growth, linking the flow of growth hormone to tissue-level differential growth through to plant level shape.
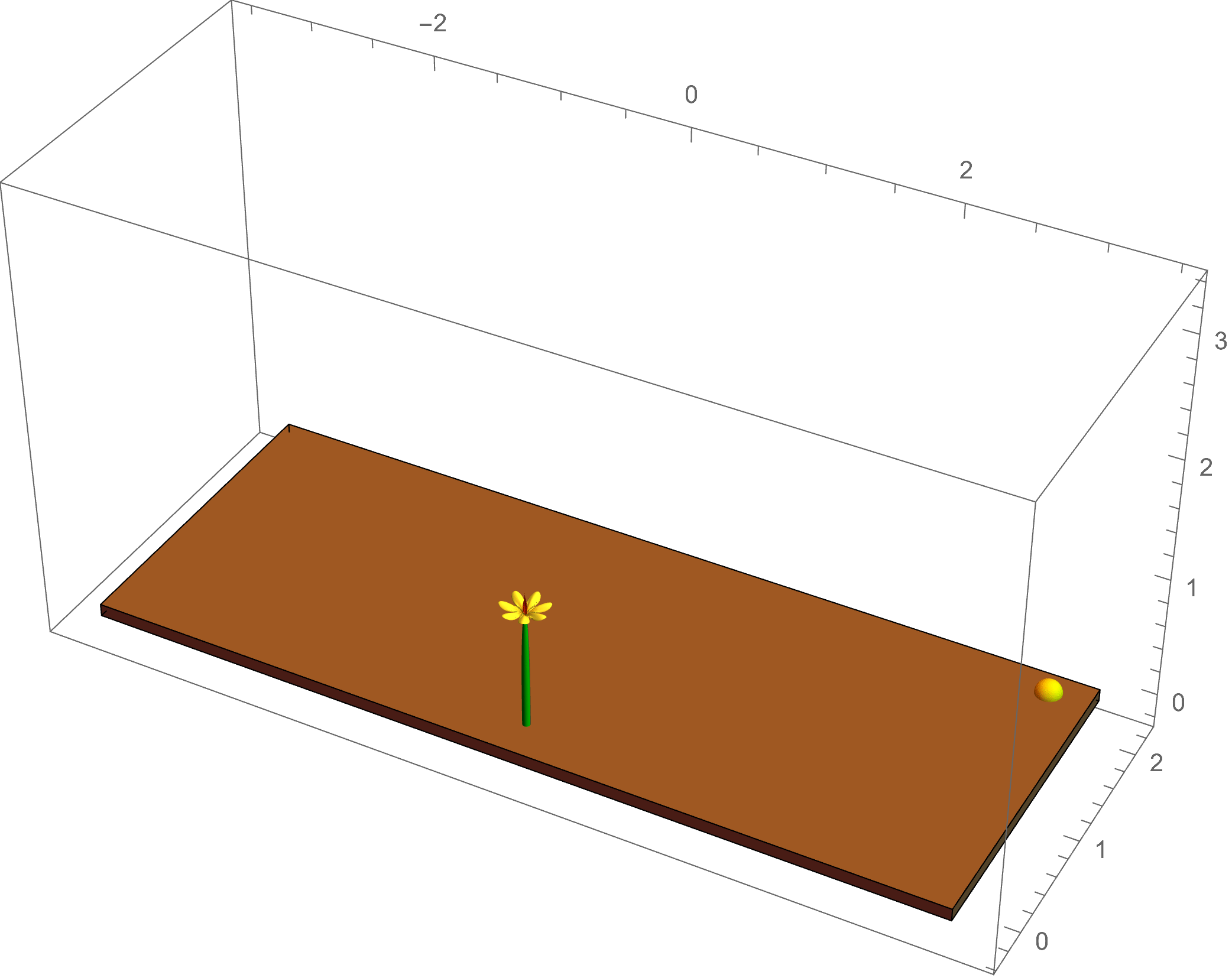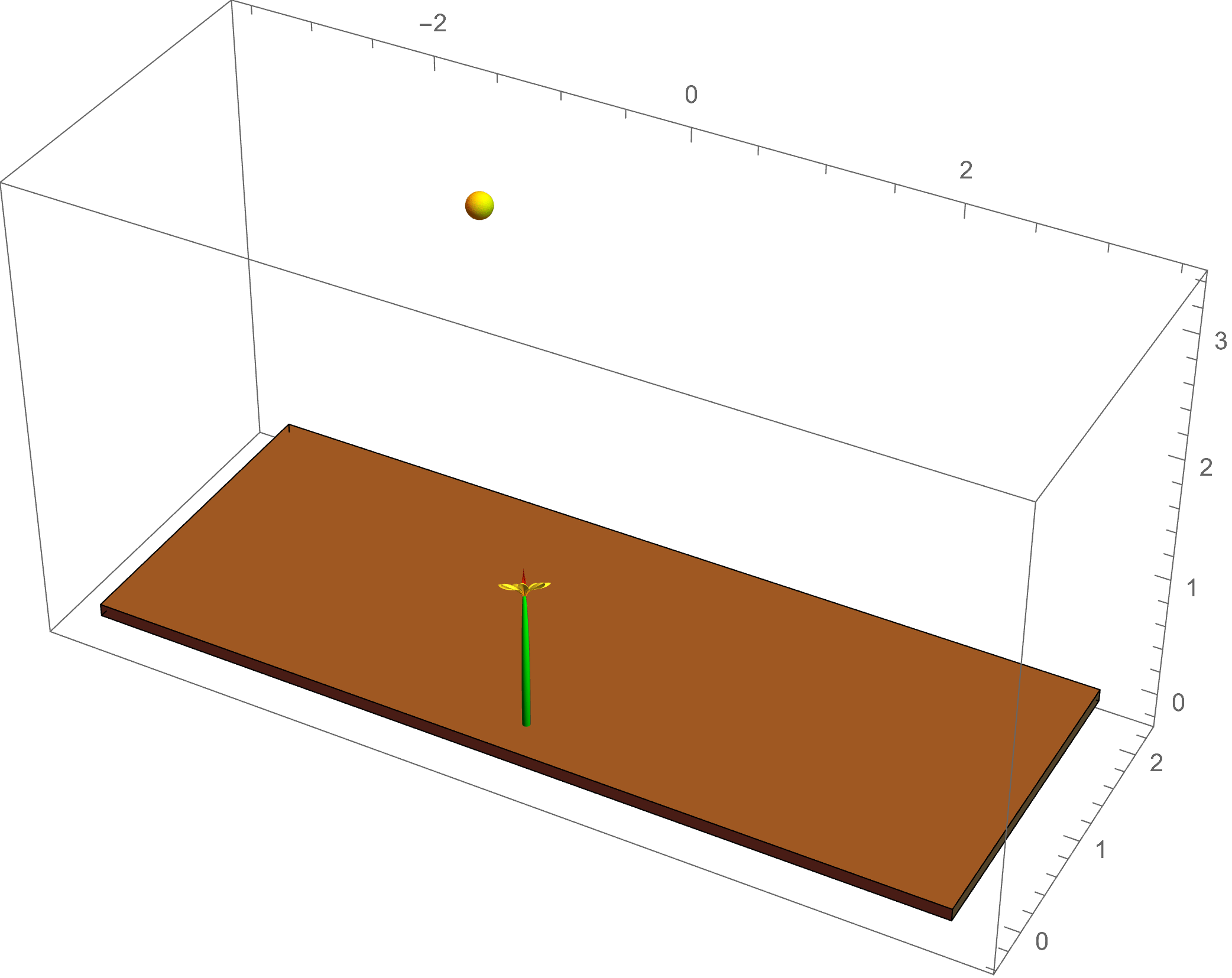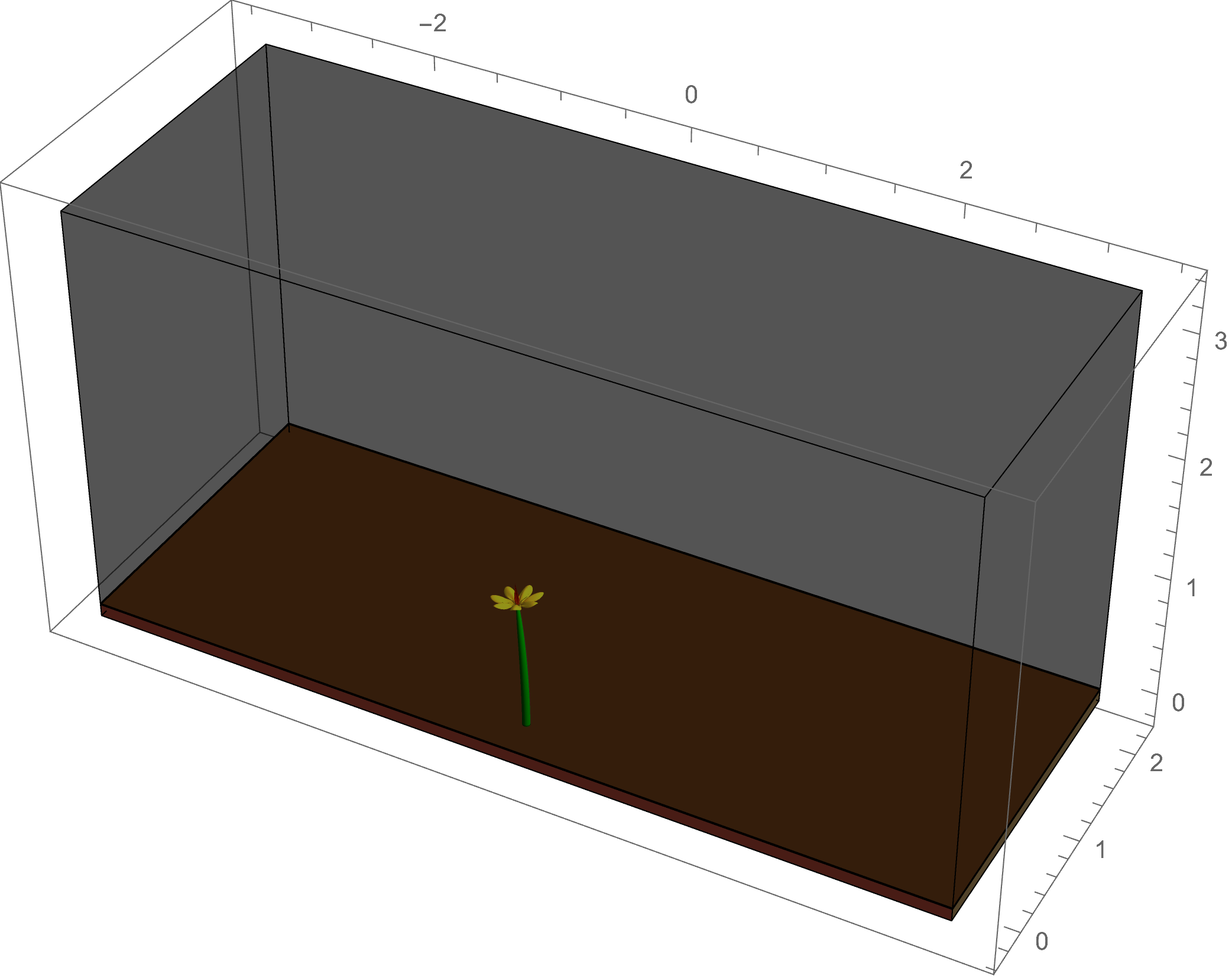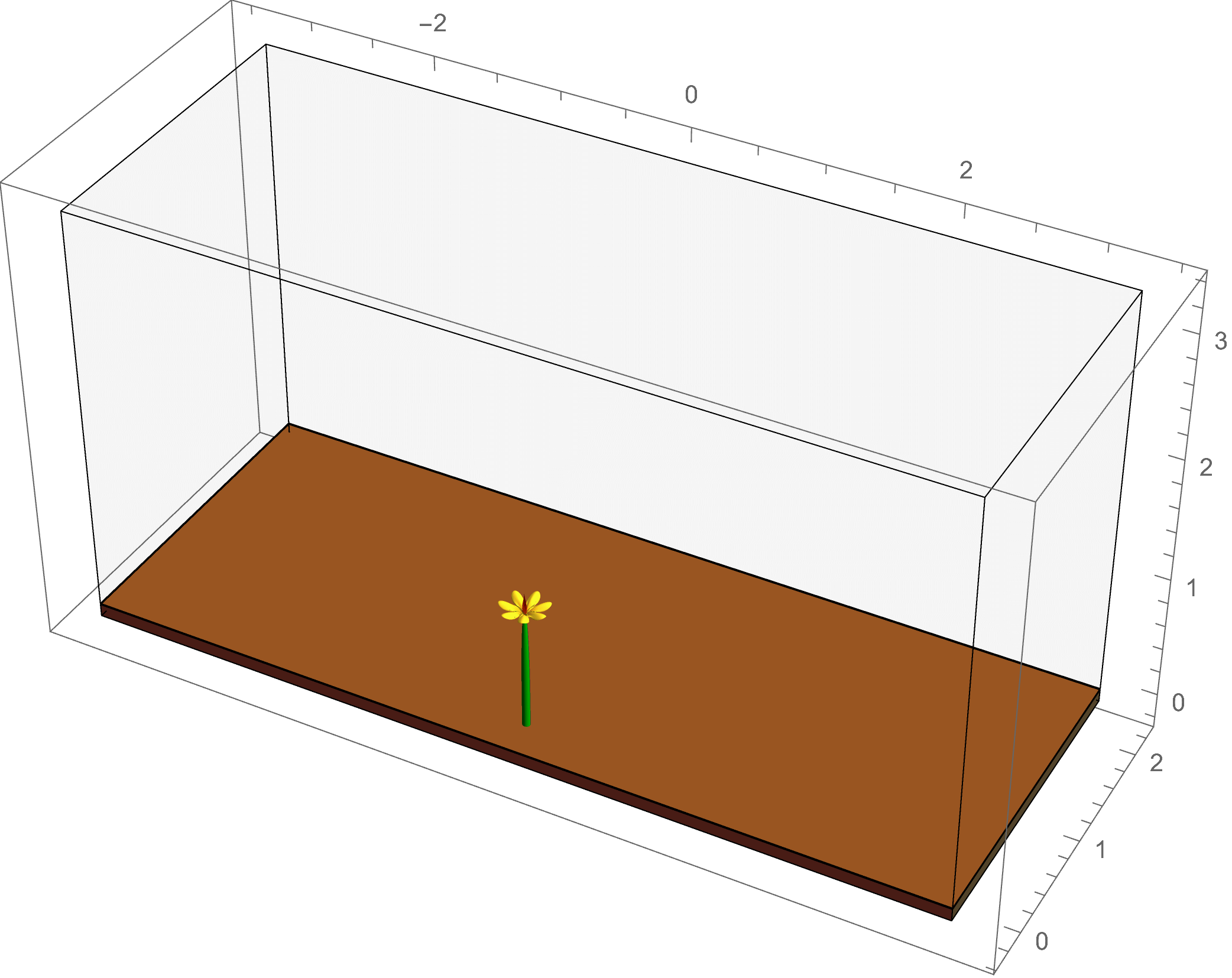The example at left shows a simulation of
phototropism: the light of the sun gives a directed signal to the plant, which causes an asymmetric flow of the growth hormone auxin; this leads to
differential growth in the plant tissue, causing a change in the intrinsic curvature of the plant stem as it bends toward the light source.
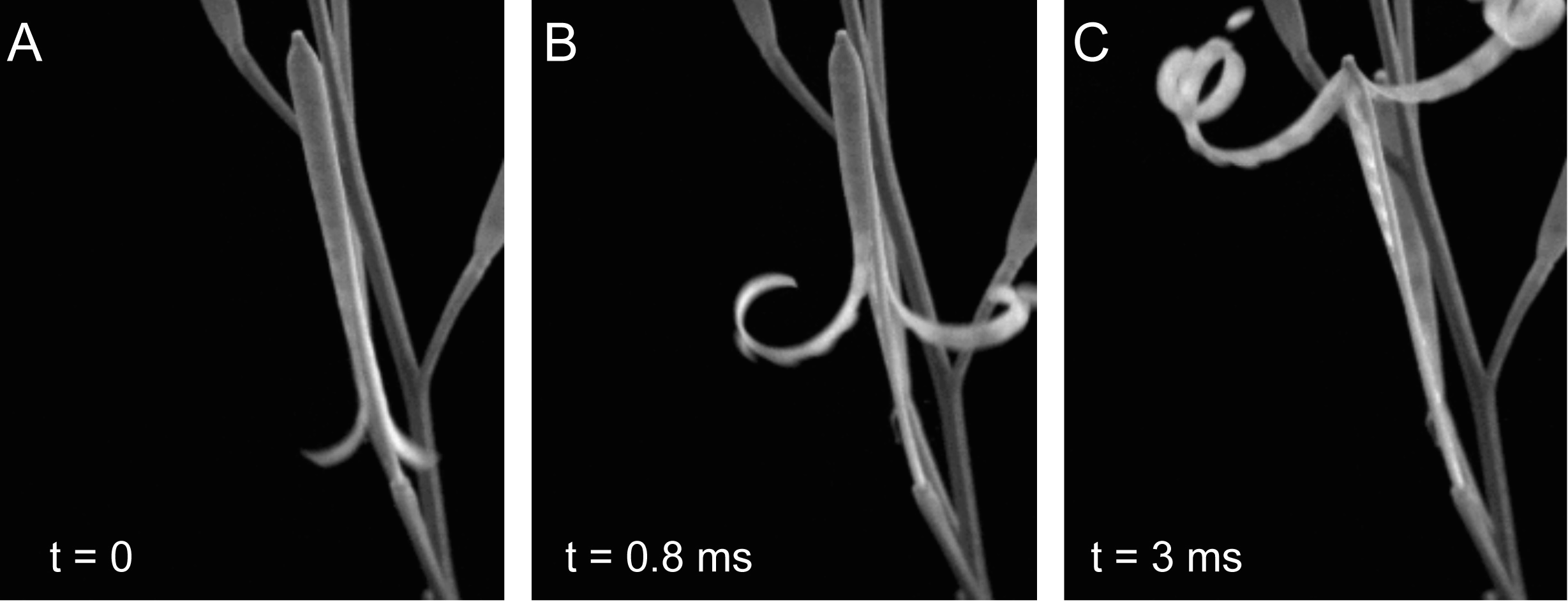
The example to the right shows
a simulation of the combined effects of circumnutation -- an oscillatory tropism used by vining plants to find something to climb -- followed by thigmotropism,
in which mechanical contact with the pole triggers an auxin flow that leads to the vine wrapping around the pole.
Everything done in the biological world requires energy, it is the fundamental unit of currency. And one of the great wonders of evolution is the multitude of solutions that have been devised for the simply stated but crucial task of motion: moving something from point A to point B. It is a trick that has been accomplished in myriad remarkable ways.
I am interested in understanding the mechanisms underlying motion in plants and animals, from various points of view:
developmental, evolutionary, and engineering design. In particular I am studying innovative uses of elastic energy,
exemplified for instance by the ballistic projection of the chameleon tongue or explosive seed dispersal in certain plants
such as Cardamine hirsuta (left).
Kidney stones, left untreated, can lead to infection and on occasion be life threatening. A common method for the removal of stones is a procedure called flexible ureterorenoscopy, in which auxiliary working tools are passed through the working channel of a tool called a ureteroscope. In laser lithotripsy, a long, thin laser fibre is passed through the ureteroscope, and shock waves fragment stones. The resulting particles and debris can obstruct the field-of-view for the operating surgeon, so a saline solution flows through the system.
This procedure involves complex and varied interactions of fluid flow, fracture mechanics, and laser physics. In collaboration with Boston Scientific and urologist Dr Ben Turney, our team has been developing a suite of mathematical models to better understand this procedure, and to aid in both the design of equipment and procedural opimisation. Papers here, here, and here.
At the level of organs, function may be found that is invisible at the level of the interacting component tissues and cells. Physiological function depends on a delicate balance between growth, stress, geometry, and external forces.
The challenge faced in modelling biological structures is finding a level of analysis sophisticated enough to characterize complexity such as inhomogeneity and anisotropy, while maintaining an ability to gain an intuitive and qualitative understanding.
I have explored such issues in the context of airways, wound healing in skin, the growth of tumour spheroids, and the mammalian bladder. The objective is to understand such systems on a mechanistic level and to find common underlying physical principles.
Elastic filaments are structures characterised by a length much greater than the cross-sectional dimensions.
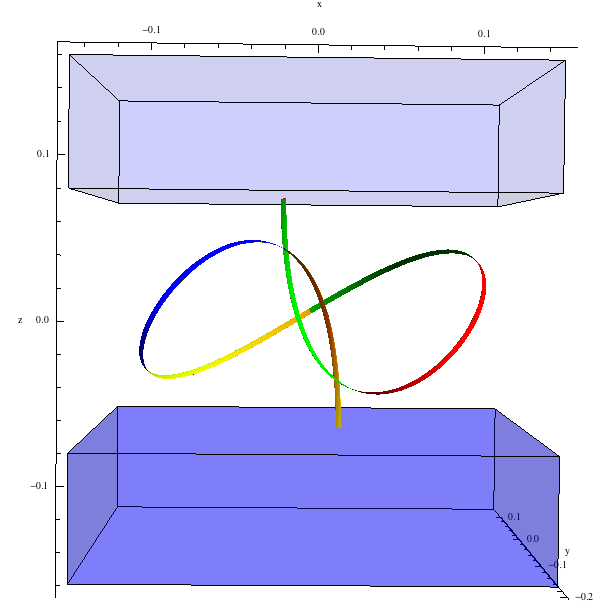
We have recently explored the stability of knotted elastic rods. In particular, we have found theoretically
for the first time a stable elastic trefoil knot with no points of self-contact, a configuration easily
demonstrated with a strip of paper, as illustrated below. As well as as increasing the understanding of the rich solution structure of
the Kirchhoff equations, knots are prominent in biopolymers such as DNA, and self-contact is an important feature.
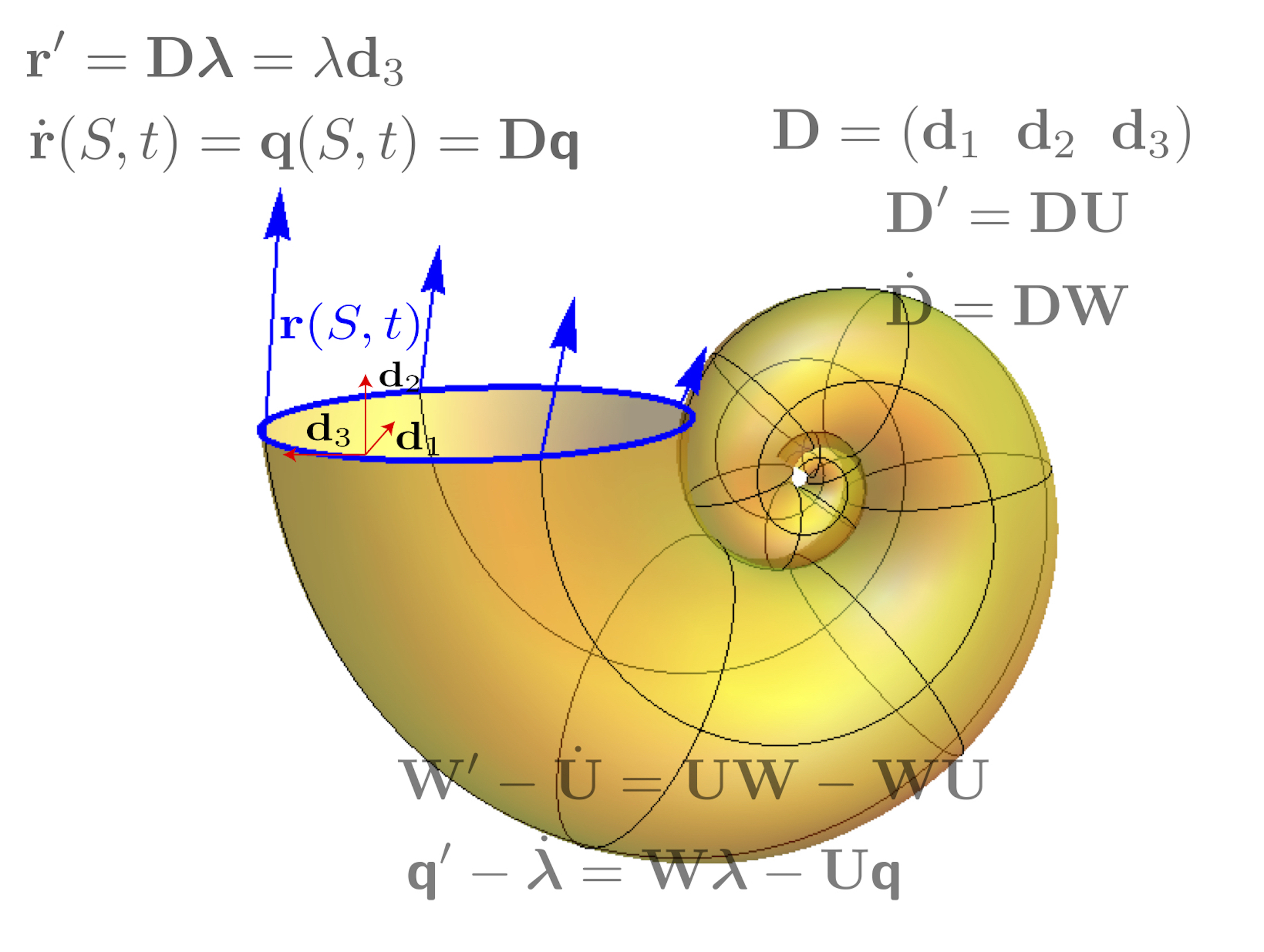
Elastic filaments are also very common in biology - for instance bacterial fibers, roots, and spine - and can have complicated 3D geometry. Understanding the mechanical behavior of these structures in the context of growth poses a significant challenge. We have developed a general framework to study such structures, which we term morphoelastic rods. Our approach combines the typical Kirchhoff equations for elastic rods with fundamental ideas from 3D morphoelasticity.
We have also extended this work to the situation of 2 connected elastic rods with potentially different mechanical properties and growing at different rates. Our framework enables complex shapes and behaviour, such as perversion of helically wound filaments, to be studied efficiently and analytically.
In the third installment of this series of work, we formally derived the link between volumetric growth in a 3D elastic cylinder and the intrinsic curvature of the same object when viewed as an elastic morphorod. This framework was the critical modelling component of our work on modelling tropic plant growth, and has strong potential in a number of other areas, such as soft robotics, and liquid crystal elastomers.
A vertical soap film draining under gravity is a classic experiment, explored since the time of Newton. In our lab at the University of Delaware, we created magnetic soap-films by adding magnetic nano-particles to a standard soap-film recipe.
We have developed a 2D model for a draining magnetic film using lubrication theory. We have captured well the basic phenomenon of reverse draining; we have also explored the effect of a disjoining pressure due to molecular forces. Pictured on the left is a regular draining soap film, on the right a magnetic film placed under a strong magnet drains upward, against gravity (the black signals the thinnest, drained region).