| Motivic action conjecture for Doi-Naganuma lifts [PDF]
[arXiv]
with Yingkun Li
submitted (2025)
We prove the motivic action conjecture for the base change to real quadratic fields of weight one newforms with odd, squarefree level and solvable projective image. |
 |
|
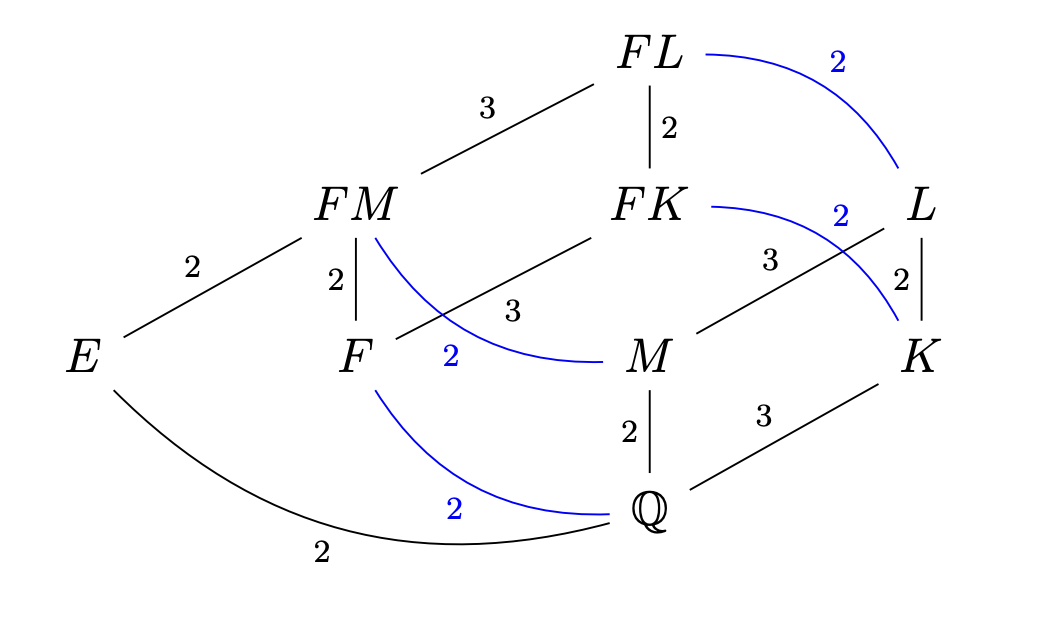
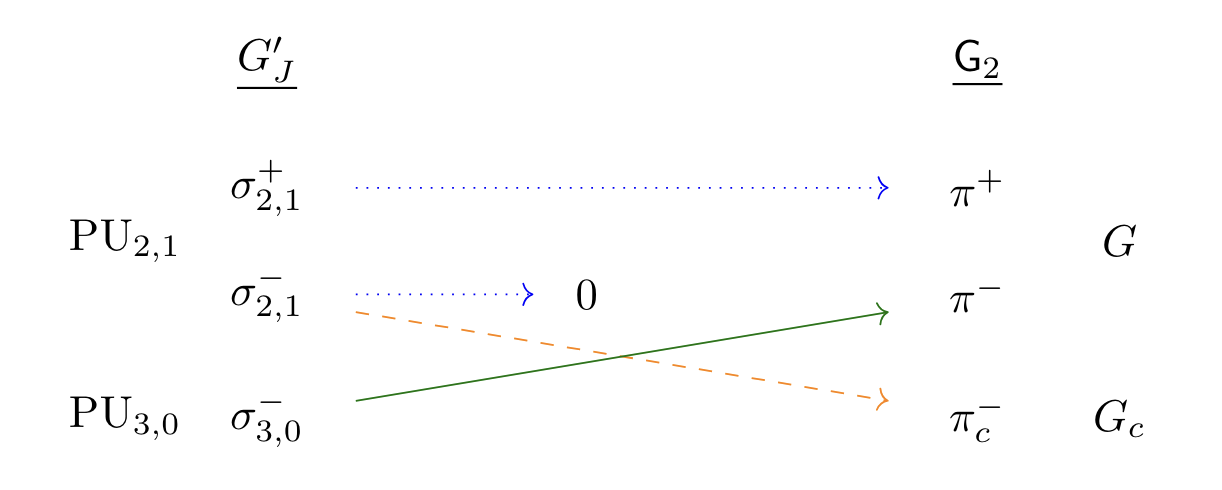
Global long root A-packets for G2: the dihedral case [PDF] [arXiv]
with Siyan Daniel Li-Huerta, Petar Bakić, and Naomi Sweeting
submitted (2024)
Cuspidal automorphic representations τ of PGL2 correspond to global long root A-parameters for G2. Using an exceptional theta lift between PU3 and G2, we construct the associated global A-packet and prove the Arthur multiplicity formula for these representations when τ is dihedral and satisfies some technical hypotheses. We also prove that this subspace of the discrete automorphic spectrum forms a full near equivalence class. Our construction yields new examples of quaternionic modular forms on G2. |
 |
|
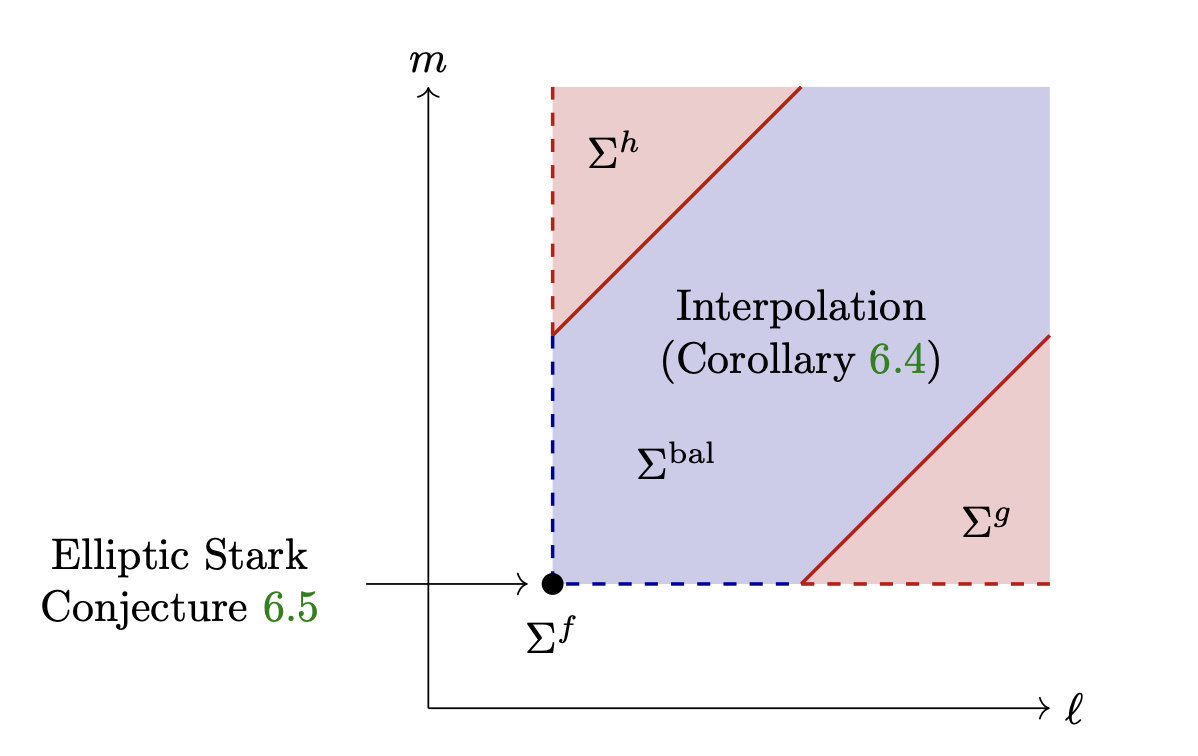
Balanced triple product p-adic L-functions and Stark points [PDF] [arXiv]
with Luca Dall'Ava
submitted (2024)
We use p-adic methods to investigate the equivariant BSD conjecture for an elliptic curve and two odd 2-dimensional Artin representations. When the rank of the relevant Mordell-Weil group is two, Darmon-Lauder-Rotger used a dominant triple product p-adic L-function to study it, and gave an Elliptic Stark Conjecture which relates its value outside of the interpolation range to two Stark points and one Stark unit. Our paper achieves a similar goal in the rank one setting. We first generalize Hsieh's construction of a 3-variable balanced triple product p-adic L-function in order to allow Hida families with classical weight one specializations. We then give an Elliptic Stark Conjecture relating its value outside of the interpolation range to a Stark point and two Stark units. We prove our conjecture for dihedral representations associated with the same imaginary quadratic field. This requires a generalization of the results of Bertolini-Darmon-Prasanna which we prove in the appendix. Video of my ICMS talk about this paper. |
 |
|
Motivic action for Siegel modular forms [PDF] [arXiv]
with Kartik Prasanna
to appear in the Journal of the European Mathematical Society (2025)
Inspired by the work of Prasanna-Venkatesh on singular cohomology of locally symmetric spaces, we propose a conjecture that explains all the contributions of Siegel modular forms of low weight to coherent cohomology in terms of the action of a motivic cohomology group. Under some technical conditions, we prove that our conjecture is equivalent to Beilinson's conjecture for the adjoint L-function of f. We also consider two special cases: for lifts of Hilbert modular forms, we prove an unconditional result towards the conjecture, and for lifts of Bianchi modular forms, we show that our conjecture is compatible with the conjecture of Prasanna-Venkatesh. The latter establishes a connection between the motivic action conjectures for locally symmetric spaces of non-hermitian type and those for coherent cohomology of Shimura varieties. Video of my online talk about this paper at the International Seminar on Automorphic Forms. Slides my short talk in Bonn, which briefly summarizes the motivic action conjectures (slide 8 gives a 1-page summary of this paper). More details are in these notes from a series of two talks I gave at Imperial College London. |
 |
|
A database of basic numerical invariants of Hilbert modular surfaces [PDF] [Journal] [arXiv]
with Eran Assaf, Angelica Babei, Ben Breen, Edgar Costa,
Avinash Kulkarni, Grant Molnar, Sam Schiavone, and John Voight
AMS Contemporary Mathematics 796 (LMFDB, Computation, and Number Theory) (2023)
We describe algorithms for computing geometric invariants for Hilbert modular surfaces, and we report on their implementation. |
 |
|
Motivic action on coherent cohomology of Hilbert modular varieties [PDF] [Journal] [arXiv]
IMRN, Volume 2023, Issue 12, June 2023, Pages 10439-10531 (2023)
We propose an action of a certain motivic cohomology group on the coherent cohomology of Hilbert modular varieties, extending conjectures of Venkatesh, Prasanna, and Harris. The action is described in two ways: on cohomology modulo p and over C, and we conjecture that they both lift to an action on cohomology with integral coefficients. The conjecture is supported by theoretical evidence based on Stark's conjecture on special values of Artin L-functions, and by numerical evidence in base change cases. Video of my Princeton/IAS Number Theory Seminar talk about this paper. Poster about (an older version of) this paper. The explication of the main conjecture is slightly different in the newest version: see slide 6 of these slides. |
 |